Skalarprodukt og vinkler

Skalarproduktet er en måde at kombinere to vektorer på, der giver et tal. Det bruges blandt andet til at bestemme vinklen mellem to vektorer og til at afgøre, om de er vinkelrette.

 

Definition

For to vektorer \( \large \mathbf{u} = (x_1,y_1) \) og \( \large \mathbf{v} = (x_2,y_2) \) gælder:

 

$$ \large \mathbf{u} \cdot \mathbf{v} = x_1 \cdot x_2 + y_1 \cdot y_2 $$

 

Derudover kan skalarproduktet skrives som:

 

$$ \large \mathbf{u} \cdot \mathbf{v} = |\mathbf{u}| \cdot |\mathbf{v}| \cdot \cos(\theta) $$

 

hvor \( \large \theta \) er vinklen mellem vektorerne.

 

 

Eksempler

Eksempel 1:

 

$$ \large \mathbf{u} = (1,0), \; \mathbf{v} = (0,1) $$

$$ \large \mathbf{u} \cdot \mathbf{v} = 1 \cdot 0 + 0 \cdot 1 = 0 $$

 

Vektorerne er ortogonale (vinkelrette), og vinklen er \( \large 90^\circ \).

 

Eksempel 2:

 

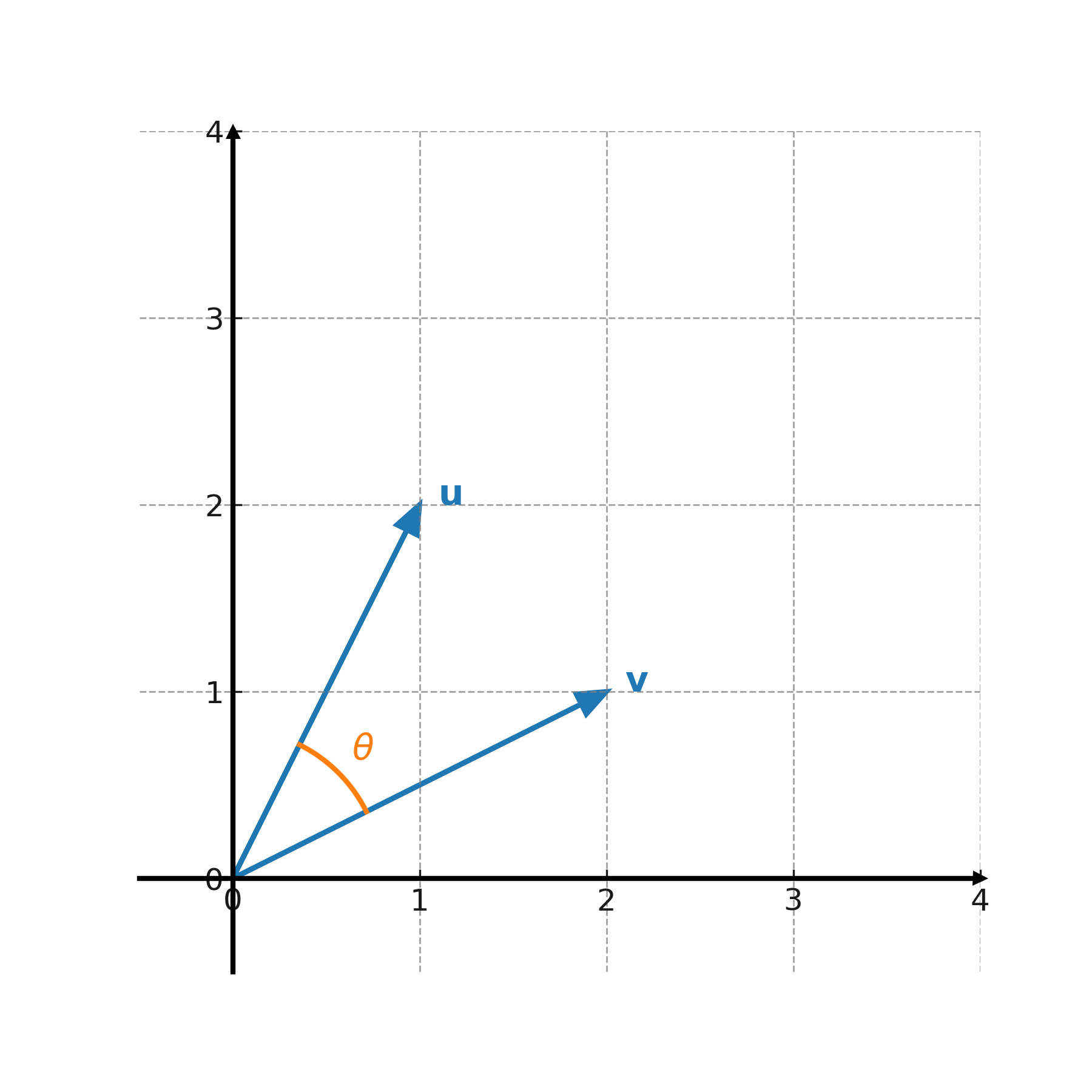
$$ \large \mathbf{u} = (1,2), \; \mathbf{v} = (2,1) $$

$$ \large \mathbf{u} \cdot \mathbf{v} = 1 \cdot 2 + 2 \cdot 1 = 4 $$

 

Længderne er \( \large |\mathbf{u}| = \sqrt{5}, \; |\mathbf{v}| = \sqrt{5} \). Dermed:

 

$$ \large \cos(\theta) = \frac{4}{\sqrt{5} \cdot \sqrt{5}} = \frac{4}{5} $$

 

Vinklen er derfor:

 

$$ \large \theta = \cos^{-1}\left(\frac{4}{5}\right) \approx 36,9^\circ $$

 

 

Geometrisk fortolkning

Skalarproduktet måler, hvor meget af den ene vektor der peger i samme retning som den anden. Hvis vinklen er spids, er produktet positivt. Hvis vinklen er stump, er produktet negativt. Hvis vinklen er ret, er produktet nul.

 

 

Anvendelse

Skalarproduktet bruges i matematik og fysik til at bestemme vinkler og til at afgøre, om vektorer er vinkelrette. I fysik bruges det også til at udregne den del af en kraft, der virker i en bestemt retning.