Addition og subtraktion

Når man arbejder med vektorer i planen, kan man lægge dem sammen eller trække dem fra hinanden. Det gøres ved at kombinere koordinaterne for hver vektor.

 

Definition

For to vektorer \( \large \mathbf{u} = (x_1,y_1) \) og \( \large \mathbf{v} = (x_2,y_2) \) gælder:

 

$$ \large \mathbf{u} + \mathbf{v} = (x_1 + x_2,\; y_1 + y_2) $$

 

$$ \large \mathbf{u} - \mathbf{v} = (x_1 - x_2,\; y_1 - y_2) $$

 

 

Eksempel

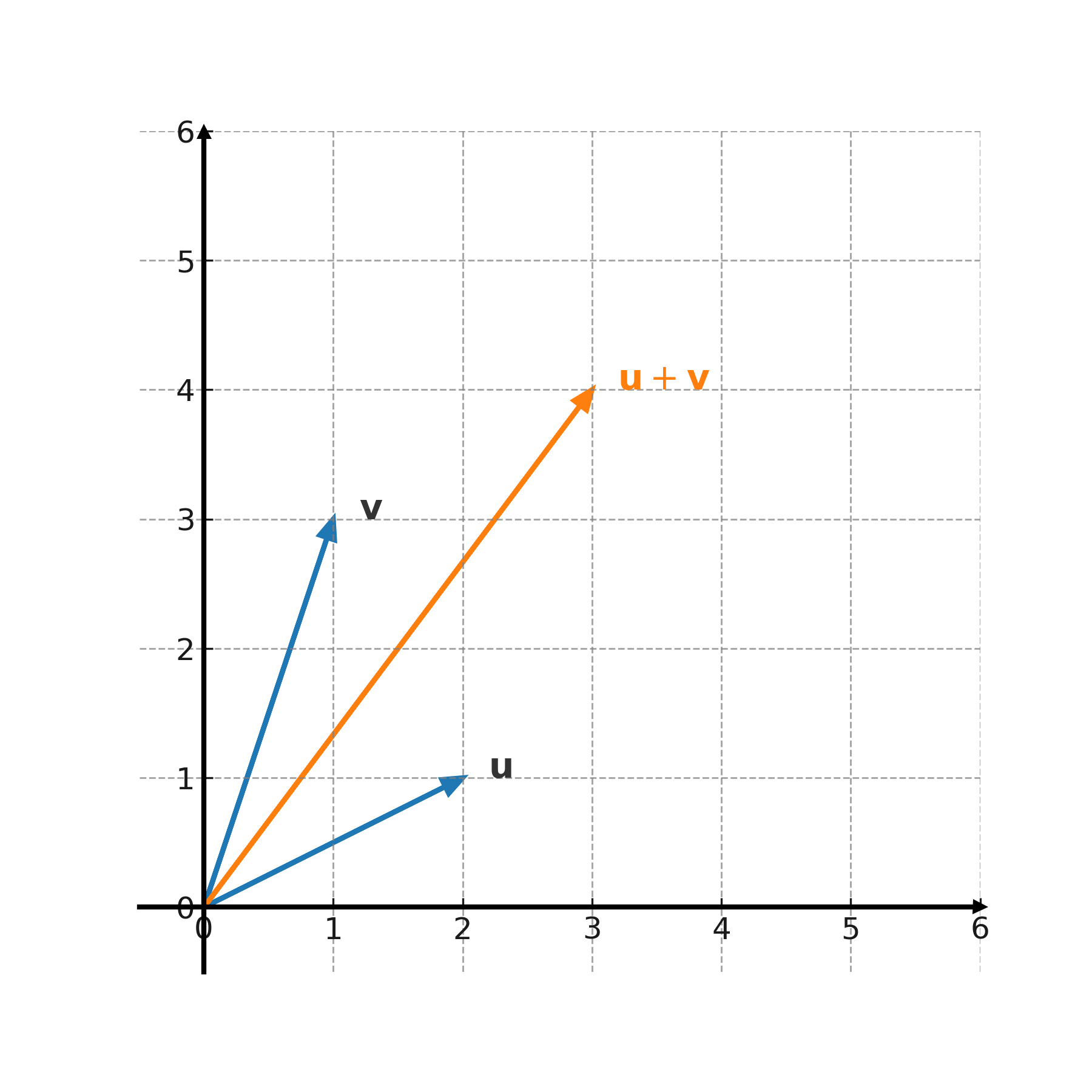
Vi vil beregne summen og differensen af vektorerne \( \large \mathbf{u} = (2,1) \) og \( \large \mathbf{v} = (1,3) \).

 

Summen bliver:

 

$$ \large (2,1) + (1,3) = (2+1,\; 1+3) = (3,4) $$

 

 

Differensen bliver:

 

$$ \large (2,1) - (1,3) = (2-1,\; 1-3) = (1,-2) $$

 

 

Geometrisk fortolkning

Additionen kan vises grafisk med parallelogrammetoden: man lægger vektorerne hale mod hale og tegner to kopier, så der dannes et parallelogram. Diagonalen repræsenterer summen.

 

 

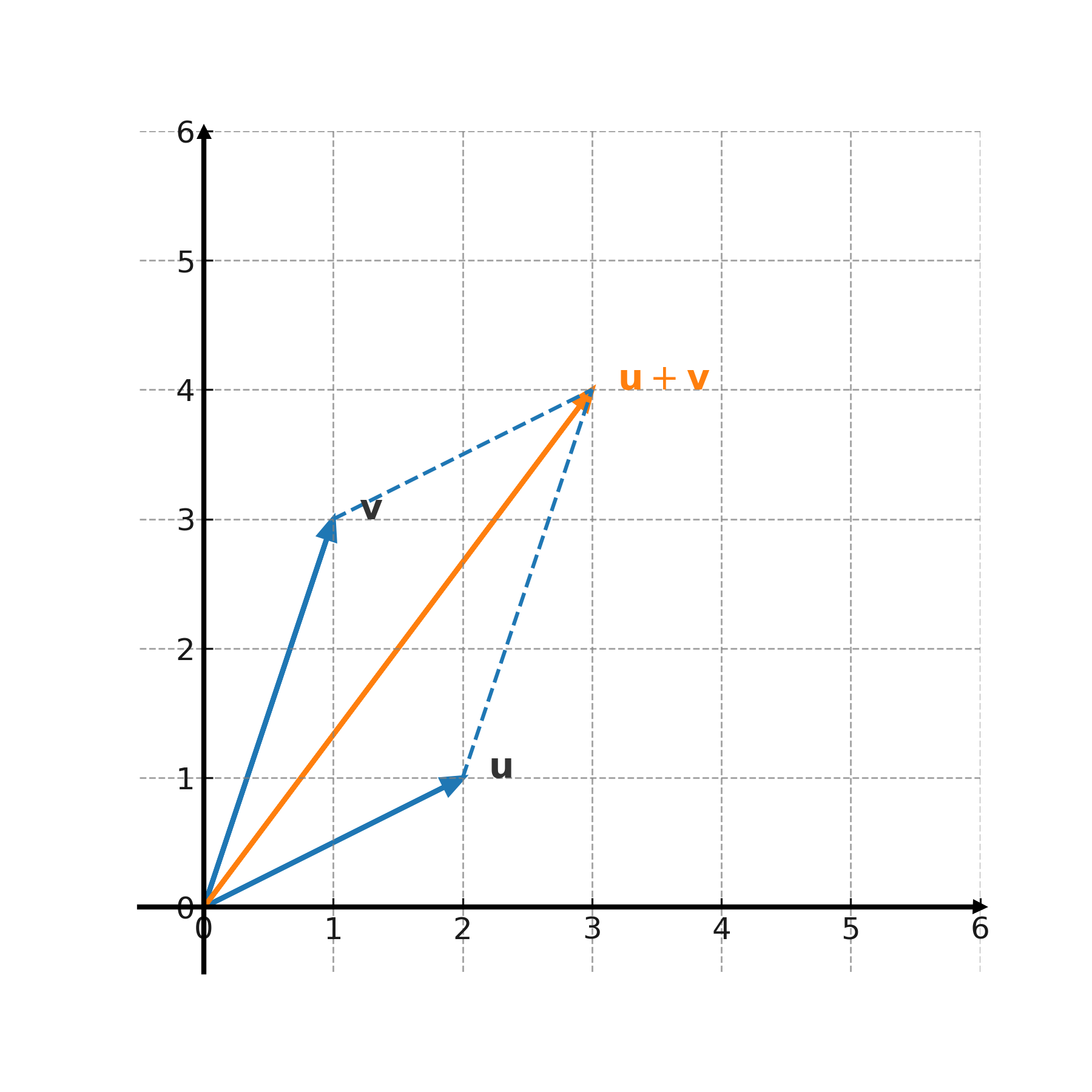
Subtraktionen kan ses som addition af den modsatte vektor. For eksempel er \( \large \mathbf{u} - \mathbf{v} = \mathbf{u} + (-\mathbf{v}) \).

 

 

Anvendelse

I fysik bruges addition af vektorer til at bestemme den samlede kraft på et legeme. Hvis en kasse trækkes i én retning af en kraft og i en anden retning af en anden kraft, er den resulterende bevægelse givet ved summen af de to kraftvektorer.