Multiplikation med tal

Når man ganger en vektor med et tal, ændres dens længde, men retningen bevares, hvis tallet er positivt. Hvis tallet er negativt, vendes vektoren om i den modsatte retning.

 

Definition

For en vektor \( \large \mathbf{v} = (x,y) \) og et tal \( \large k \) gælder:

 

$$ \large k \cdot (x,y) = (k \cdot x,\; k \cdot y) $$

 

Eksempler

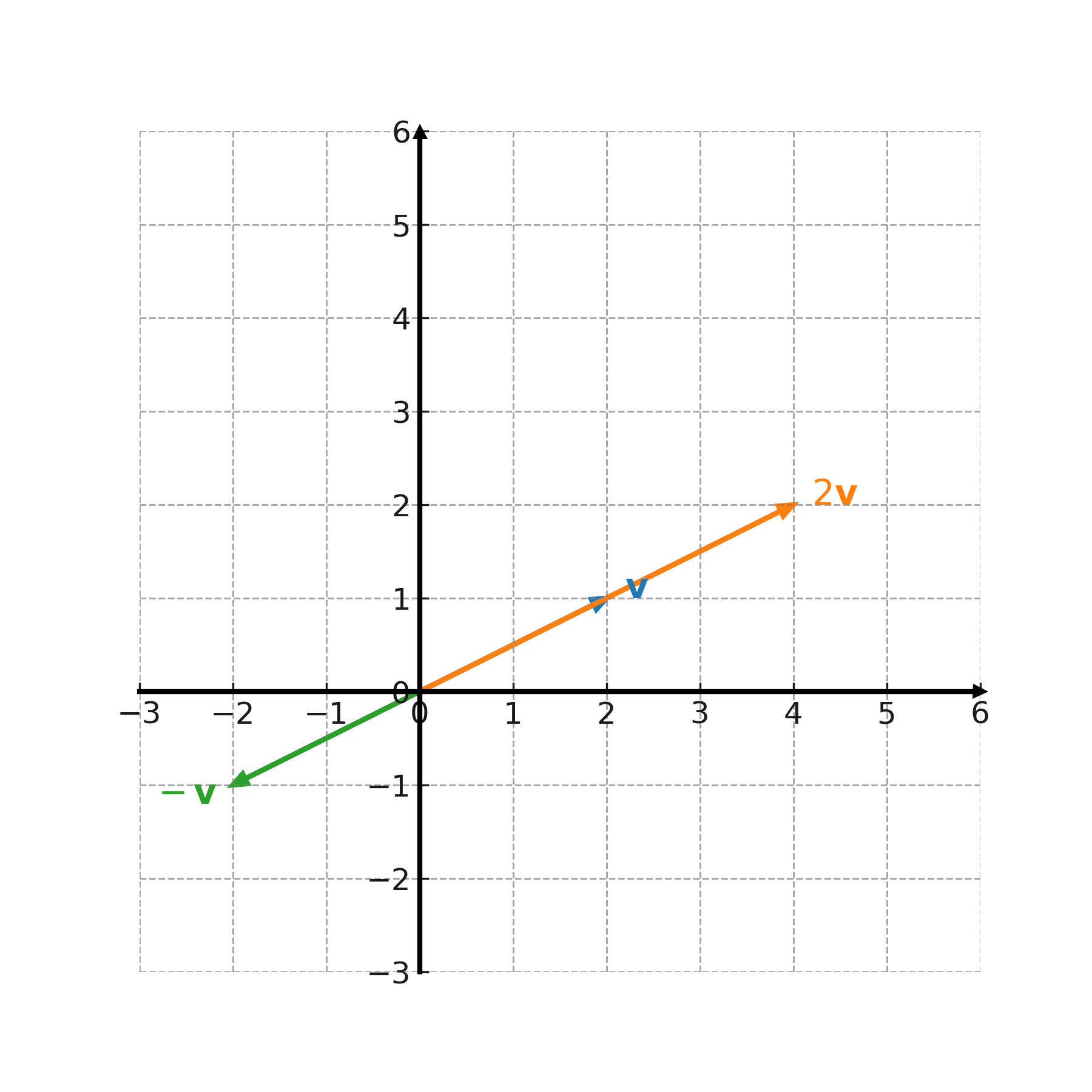
Vi ser på vektoren \( \large \mathbf{v} = (2,1) \).

 

Når \( \large k = 2 \):

$$ \large 2 \cdot (2,1) = (4,2) $$

 

Når \( \large k = -1 \):

$$ \large -1 \cdot (2,1) = (-2,-1) $$

 

Når \( \large k = \frac{1}{2} \):

$$ \large \frac{1}{2} \cdot (2,1) = (1,\; \frac{1}{2}) $$

 

Når \( \large k = 0 \):

$$ \large 0 \cdot (2,1) = (0,0) $$

 

Geometrisk fortolkning

Multiplikation med et tal strækker eller formindsker vektoren. For positive tal bevares retningen, for negative tal vendes retningen om. Når tallet er mellem 0 og 1, bliver vektoren kortere, og når tallet er 0, fås nulvektoren.

 

 

Anvendelse

Multiplikation med tal bruges til at ændre størrelse på en bevægelse eller kraft. I fysik svarer det til at ændre styrken af en kraft uden at ændre retningen.

 

I matematik anvendes multiplikation med parametre til at beskrive linjer og kurver, for eksempel \( \large (x,y) = (x_0,y_0) + t \cdot \mathbf{r} \), hvor \( \large t \) er et tal og \( \large \mathbf{r} \) en retningsvektor.