Areal med vektorer

Arealet af en figur kan beregnes ved hjælp af vektorer. Særligt parallelogrammer og trekanter kan udtrykkes på en enkel formel, når de beskrives af to vektorer.

 

 

Areal af parallelogram og trekant

For to vektorer \( \large \mathbf{u} \) og \( \large \mathbf{v} \) i planen gælder, at arealet af parallelogrammet udspændt af dem er:

 

$$ \large A = |\mathbf{u}| \cdot |\mathbf{v}| \cdot \sin(\theta) $$

 

hvor \( \large \theta \) er vinklen mellem vektorerne. Formlen kommer fra at beregne grundlinje gange højde, hvor højden findes som projektionen af den ene vektor på en retning vinkelret på den anden.

 

En anden metode er at bruge determinanten:

 

$$ \large A = \left| \det \begin{pmatrix} x_1 & x_2 \\ y_1 & y_2 \end{pmatrix} \right| $$

 

hvis \( \large \mathbf{u} = (x_1,y_1) \) og \( \large \mathbf{v} = (x_2,y_2) \).

 

 

Eksempel

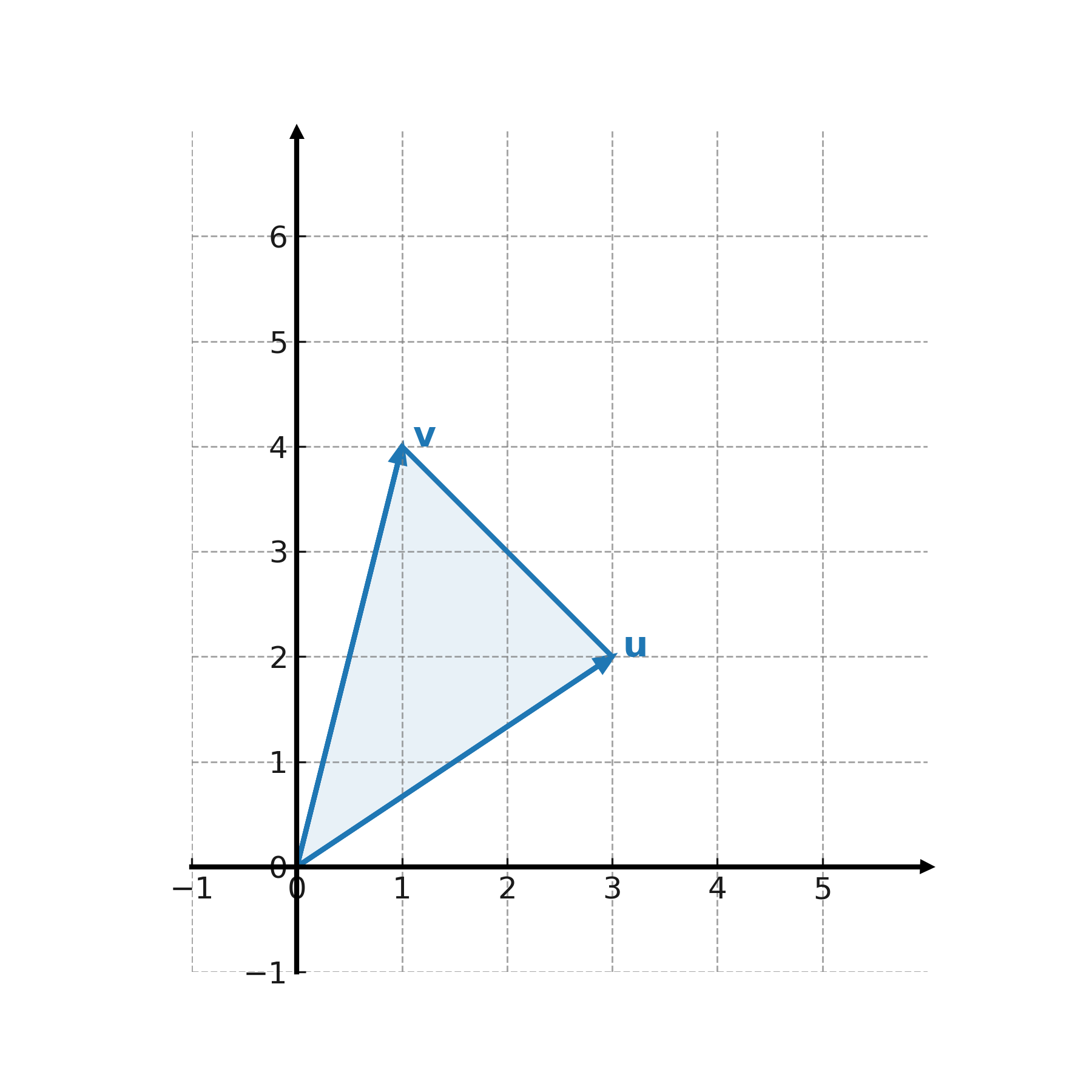
Vi tager \( \large \mathbf{u} = (3,2) \) og \( \large \mathbf{v} = (1,4) \).

 

$$ \large A = \left| \det \begin{pmatrix} 3 & 1 \\ 2 & 4 \end{pmatrix} \right| = |3 \cdot 4 - 2 \cdot 1| = |10| = 10 $$

 

Arealet af parallelogrammet er 10. 

Arealet af trekanten udspændt af de samme to vektorer er halvdelen, altså \( \large 5 \).

 

 

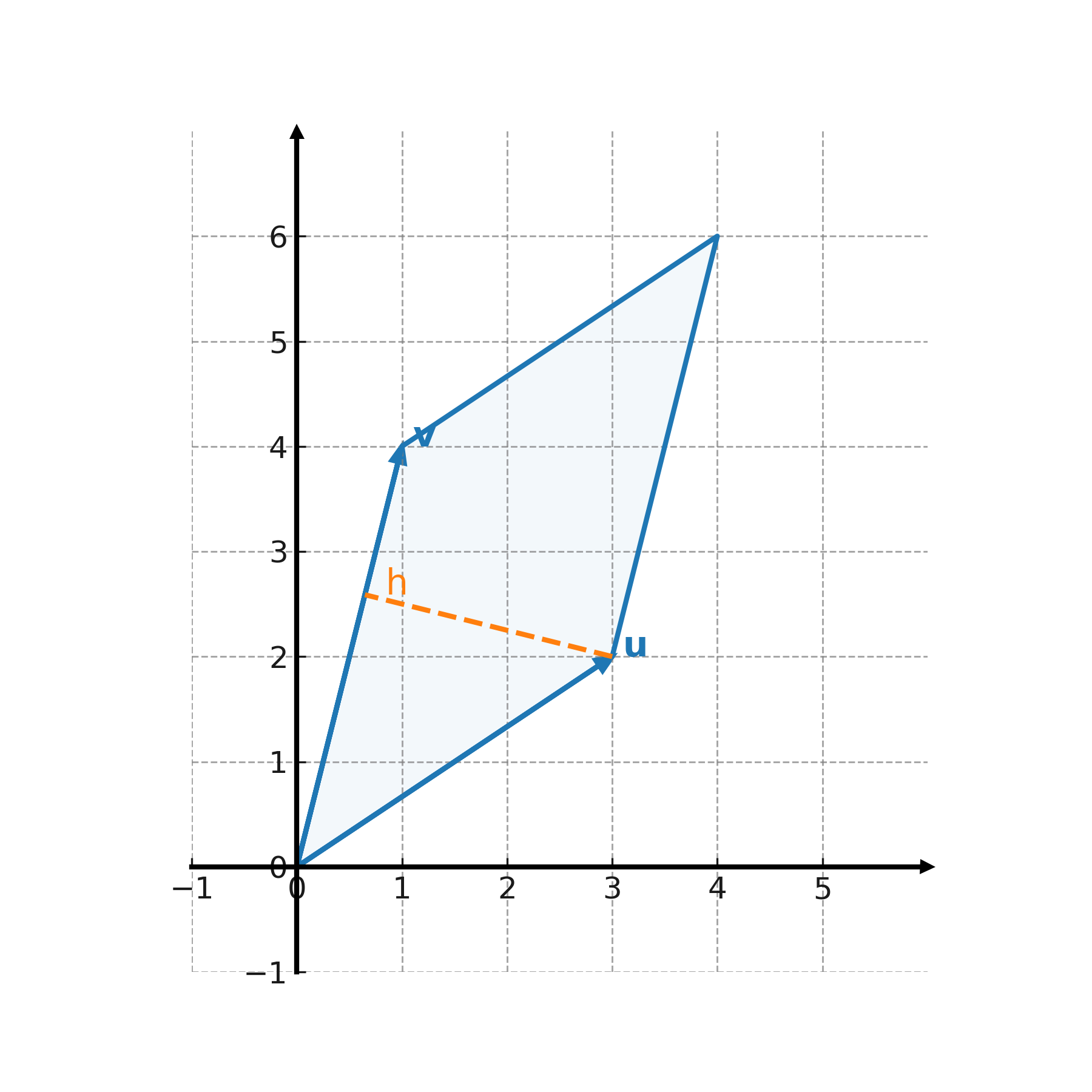
Geometrisk fortolkning

Det vigtigste at bemærke er, at arealet kan beregnes som grundlinje gange højde, og at højden kan findes ved hjælp af projektion. Dermed hænger begrebet projektion tæt sammen med arealberegning.

 

 

Anvendelse

Vektorbaserede formler for arealer bruges i både geometri og lineær algebra. De giver en enkel metode til at beregne arealer i koordinatsystemer og danner grundlag for videre emner som determinanter og rumfang.