Længde og enhedsvektorer
Længden af en vektor beskriver, hvor stor vektoren er, mens en enhedsvektor er en vektor med længden 1 i samme retning som den oprindelige.
Længde
For en vektor \( \large \mathbf{v} = (x,y) \) findes længden ved:
$$ \large |\mathbf{v}| = \sqrt{x^2 + y^2} $$
Eksempel: Vektoren \( \large \mathbf{v} = (3,4) \) har længden
$$ \large |\mathbf{v}| = \sqrt{3^2 + 4^2} = 5 $$
Enhedsvektor
En enhedsvektor findes ved at dividere en vektor med dens længde:
$$ \large \mathbf{e} = \frac{1}{|\mathbf{v}|} \cdot \mathbf{v} $$
Eksempel: For \( \large \mathbf{v} = (3,4) \) fås
$$ \large \mathbf{e} = \frac{1}{5} \cdot (3,4) = \left(\frac{3}{5}, \frac{4}{5}\right) $$
Bemærk: Nulvektoren \( \large (0,0) \) kan ikke gøres til enhedsvektor, fordi dens længde er 0, og man kan ikke dividere med 0.
De mest kendte enhedsvektorer er standardenhedsvektorerne i koordinatsystemet:
$$ \large \mathbf{i} = (1,0), \quad \mathbf{j} = (0,1) $$
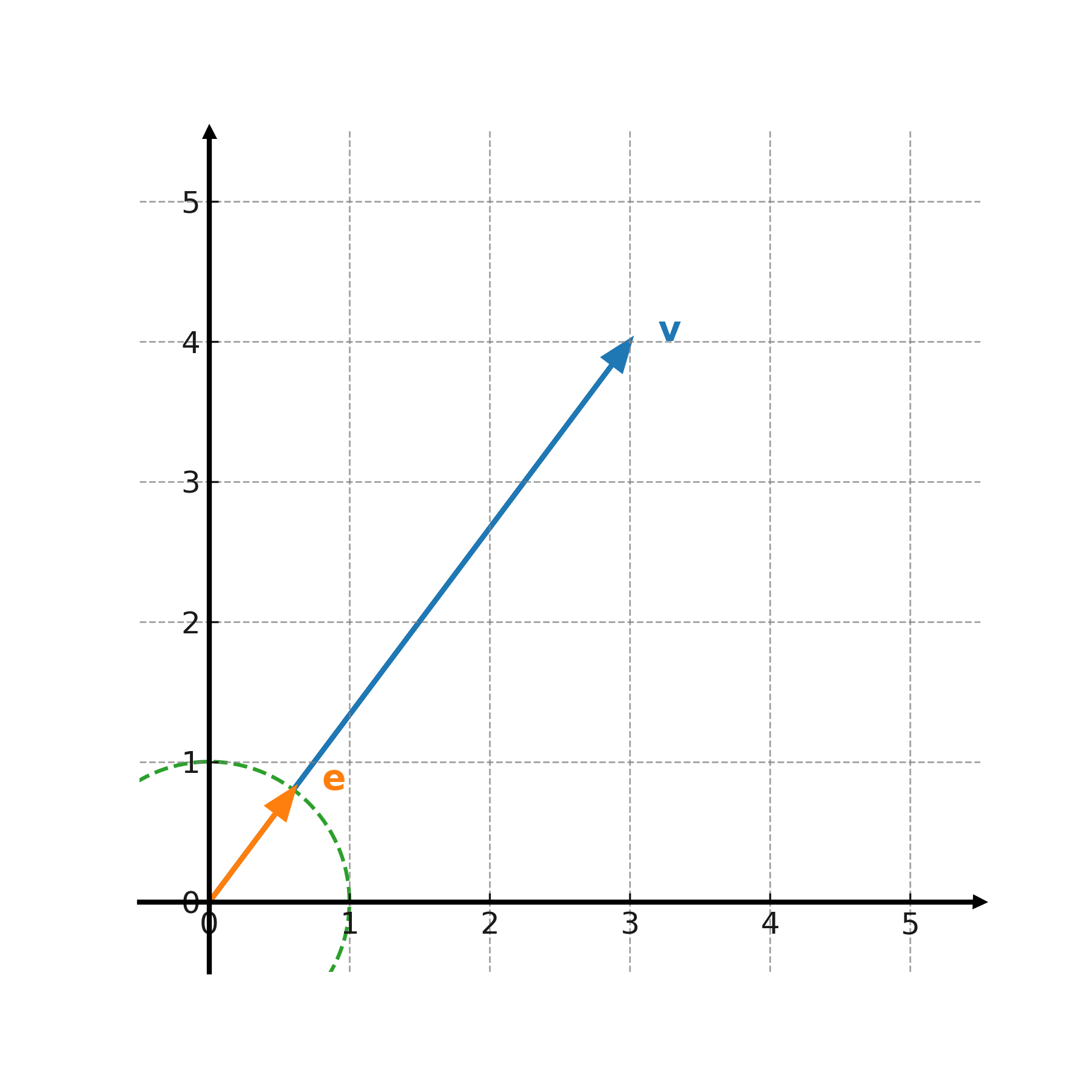
Geometrisk fortolkning
Længden af en vektor svarer til afstanden fra origo til vektorens endepunkt.
En enhedsvektor er en pil i samme retning, men altid med længden 1.
Anvendelse
Enhedsvektorer bruges til at beskrive retninger, uden at størrelsen betyder noget. I fysik bruges de for eksempel til at angive retningen af en kraft uafhængigt af dens styrke, og i matematik bruges de til at definere koordinatsystemers akser.