Trapezmetoden

Trapezmetoden er en enkel numerisk metode til at beregne en tilnærmet værdi af et bestemt integral. Den bygger på ideen om at erstatte grafen for en funktion med rette linjer, så området under kurven kan beregnes som summen af trapezer.

 

 

Idéen bag metoden

Når man ikke kan finde det eksakte integral \( \large \int_a^b f(x)\,dx \), kan man i stedet opdele intervallet \( \large [a,b] \) i \( \large n \) mindre delintervaller. På hvert delinterval erstattes funktionen med en ret linje mellem de to endepunkter. Arealet under denne linje er et trapez, som er let at beregne.

 

 

Formel for trapezmetoden

For et interval opdelt i \( \large n \) lige store dele med bredde \( \large h = \frac{b-a}{n} \) gælder:

 

$$ \large \int_a^b f(x)\,dx \approx \frac{h}{2} \left[f(x_0) + 2f(x_1) + 2f(x_2) + \ldots + 2f(x_{n-1}) + f(x_n)\right] $$

 

 

Trinvis fremgangsmåde

 

1. Opdel intervallet \( \large [a,b] \) i \( \large n \) lige store dele.
2. Beregn \( \large h = \frac{b-a}{n} \).
3. Beregn funktionsværdierne \( \large f(x_0), f(x_1), \ldots, f(x_n) \).
4. Indsæt værdierne i trapezformlen.

 

 

Eksempel

Vi vil beregne det tilnærmende areal under funktionen \( \large f(x) = x^2 \) på intervallet \( \large [0,2] \) ved at bruge 4 trapezer.

 

Her er \( \large a = 0 \), \( \large b = 2 \) og \( \large n = 4 \), så \( \large h = \frac{2-0}{4} = 0{,}5 \).

 

Funktionsværdierne er:

 

$$ \large f(0)=0, \quad f(0{,}5)=0{,}25, \quad f(1)=1, \quad f(1{,}5)=2{,}25, \quad f(2)=4 $$

 

Trapezformlen giver:

 

$$ \large A \approx \frac{0{,}5}{2}\,[0 + 2(0{,}25 + 1 + 2{,}25) + 4] = 2{,}75 $$

 

Det eksakte integral er \( \large \int_0^2 x^2\,dx = \frac{8}{3} \approx 2{,}67 \), så metoden giver en god tilnærmelse.

 

 

 

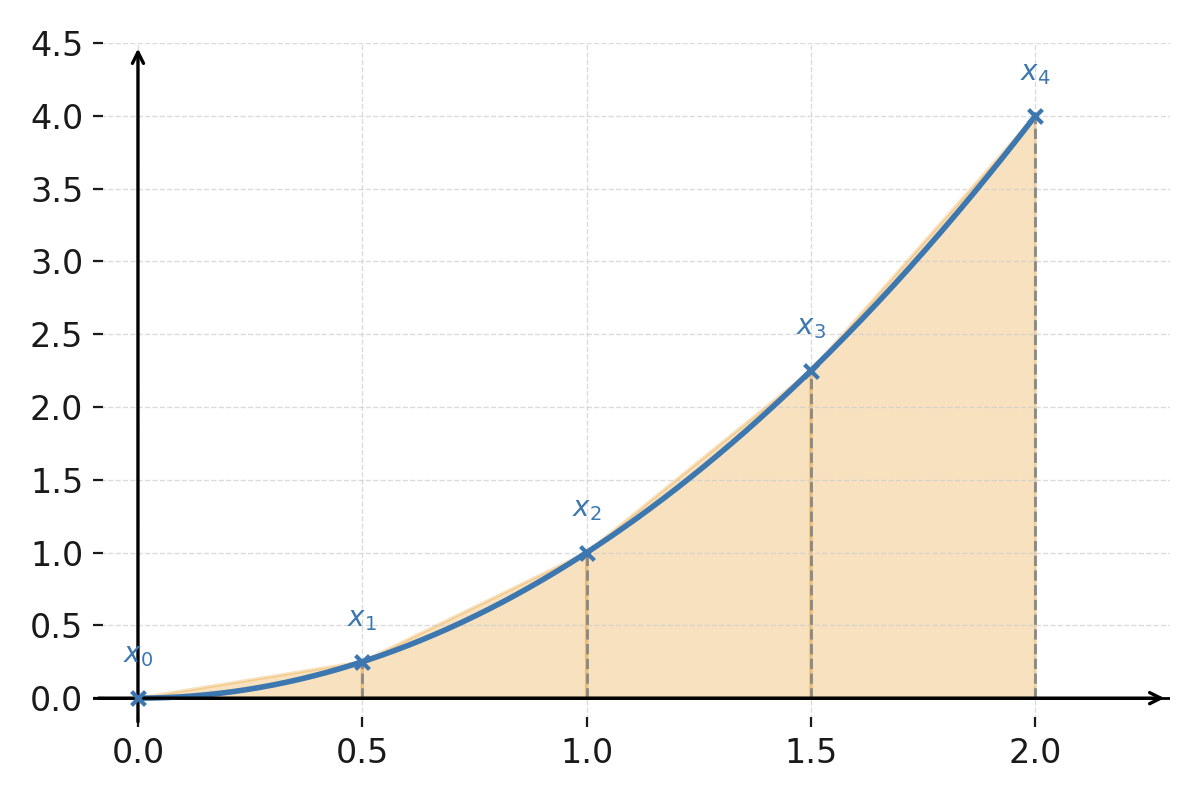
Funktionen \( \large f(x) = x^2 \) på intervallet \( \large [0,2] \).

De fire delintervaller er markeret med lodrette stiplede linjer, og de tilhørende trapezer ses mellem kurven og x-aksen. 

 

 

Bemærkninger

Trapezmetoden er nem at implementere og giver ofte en god nøjagtighed, men den kan undervurdere eller overvurdere arealet, afhængigt af om funktionen er konveks eller konkav. Nøjagtigheden kan forbedres ved at bruge flere delintervaller eller ved at anvende Simpsons regel.