Sekantmetoden

Sekantmetoden er en numerisk metode til at finde en rod i en funktion, dvs. et punkt hvor \( \large f(x) = 0 \). Den minder om Newton-Raphson-metoden, men i stedet for at bruge den afledte \( \large f'(x) \), erstattes tangenten af en sekant gennem to punkter på grafen.

 

 

Idéen bag metoden

Ved hvert trin bruges de to seneste punkter \( \large (x_{n-1}, f(x_{n-1})) \) og \( \large (x_n, f(x_n)) \) til at opstille en ret linje (sekant). Skæringspunktet mellem sekanten og x-aksen bruges som nyt gæt \( \large x_{n+1} \). Metoden gentages, indtil to på hinanden følgende gæt ligger meget tæt.

 

 

Formel

 

$$ \large x_{n+1} = x_n - f(x_n) \cdot \frac{x_n - x_{n-1}}{f(x_n) - f(x_{n-1})} $$

 

 

Trinvis fremgangsmåde

 

1. Vælg to startværdier \( \large x_0 \) og \( \large x_1 \), hvor funktionen har modsat fortegn.
2. Beregn \( \large f(x_0) \) og \( \large f(x_1) \).
3. Brug formlen til at finde \( \large x_2 \).
4. Gentag beregningen, så \( \large x_{n+1} \) beregnes ud fra de to seneste punkter \( \large x_{n} \) og \( \large x_{n-1} \).
5. Stop, når \( \large |x_{n+1} - x_n| < \varepsilon \).

 

 

Eksempel

Vi søger roden til \( \large f(x) = x^3 - x - 2 \).

 

Vælg \( \large x_0 = 1 \) og \( \large x_1 = 2 \).

 

$$ \large f(1) = -2, \quad f(2) = 4 $$

 

$$ \large x_2 = 2 - 4 \cdot \frac{2 - 1}{4 - (-2)} $$

$$ \large x_2= 2 - 4 \cdot \frac{1}{6} $$

$$ \large x_2 = 1{,}333 $$

 

Det nye punkt \( \large x_2 = 1{,}333 \) bruges sammen med \( \large x_1 = 2 \) til at beregne næste værdi:

 

$$ \large x_3 = 1{,}333 - f(1{,}333) \cdot \frac{1{,}333 - 2}{f(1{,}333) - f(2)} $$

 

Efter et par iterationer fås en rod \( \large x \approx 1{,}521 \), samme resultat som med Newton-Raphson, men uden at kende den afledte funktion.

 

 

 

 

 

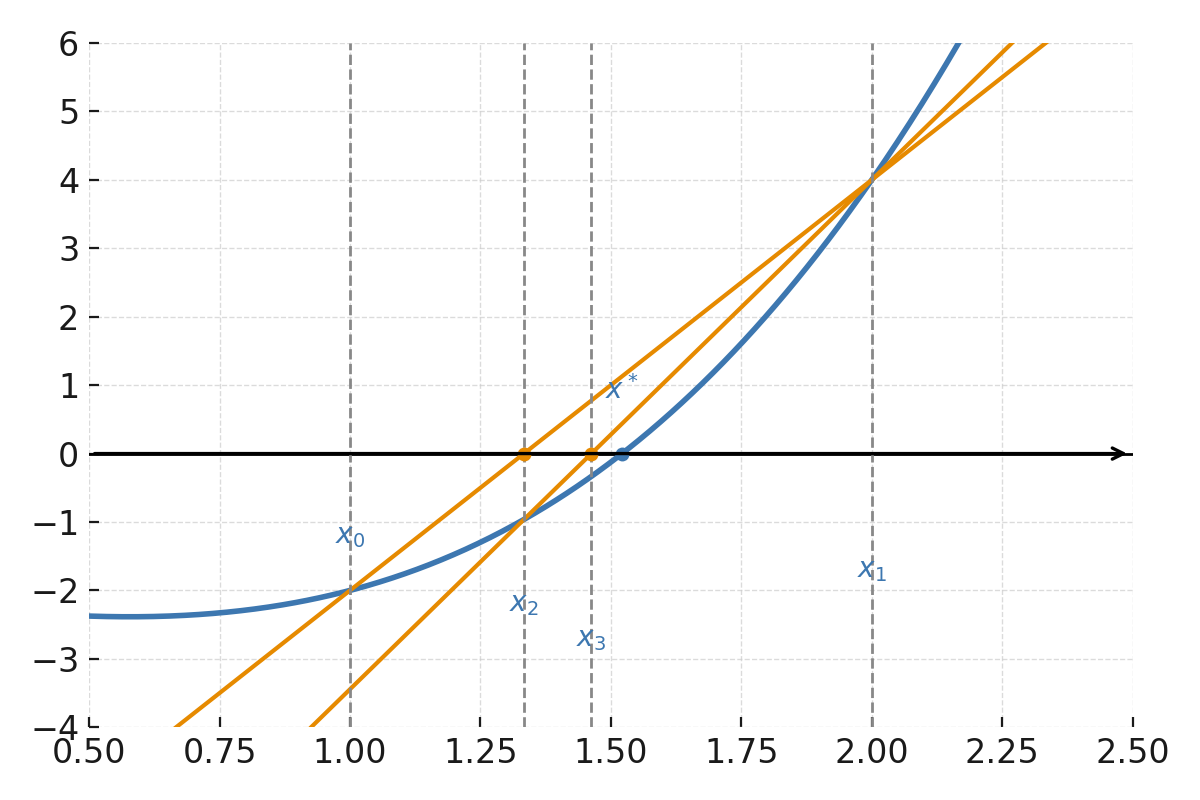
Funktionen \( \large f(x) = x^3 - x - 2 \).

Punkterne \( \large (x_0, f(x_0)) \) og \( \large (x_1, f(x_1)) \) forbindes med en  sekant, som skærer x-aksen i \( \large x_2 \). Derefter forbindes en ny sekant mellem \( \large (x_1, f(x_1)) \) og \( \large (x_2, f(x_2)) \), som skærer aksen endnu tættere på roden.

 

 

Bemærkninger

Sekantmetoden konvergerer hurtigere end halveringsmetoden, men langsommere end Newton-Raphson. Den er dog ofte et godt kompromis, fordi den ikke kræver beregning af den afledte funktion.