Simpsons regel

Simpsons regel er en forbedring af trapezmetoden til at beregne et bestemt integral numerisk. Hvor trapezmetoden erstatter funktionen med rette linjer, bruger Simpsons regel i stedet parabler (andengradspolynomier) til at tilnærme kurven. Det giver en meget bedre nøjagtighed, selv med få delintervaller.

 

 

Idéen bag metoden

Antag at vi vil beregne arealet under funktionen \( \large f(x) \) mellem \( \large a \) og \( \large b \). Intervallet opdeles i et lige antal delintervaller (for eksempel \( \large n = 4 \)). På hvert sæt af to delintervaller tegnes en parabel, som går gennem de tre punkter \( \large (x_{2i}, f(x_{2i})) \), \( \large (x_{2i+1}, f(x_{2i+1})) \) og \( \large (x_{2i+2}, f(x_{2i+2})) \). Summen af arealerne under disse parabler giver en tilnærmelse til det samlede integral.

 

 

Formel for Simpsons regel

Hvis \( \large n \) er et lige antal, og delbredderne er \( \large h = \frac{b-a}{n} \), så gælder:

 

$$ \large \int_a^b f(x)\,dx \approx \frac{h}{3}\,[f(x_0) + 4f(x_1) + 2f(x_2) + 4f(x_3) + \ldots + 4f(x_{n-1}) + f(x_n)] $$

 

Trinvis fremgangsmåde

 

1. Opdel intervallet \( \large [a,b] \) i et lige antal delintervaller \( \large n \).
2. Beregn \( \large h = \frac{b-a}{n} \).
3. Beregn funktionsværdierne \( \large f(x_0), f(x_1), \ldots, f(x_n) \).
4. Indsæt værdierne i Simpsons formel.

 

 

Eksempel

Vi beregner det tilnærmende areal under \( \large f(x) = x^2 \) på intervallet \( \large [0,2] \) med \( \large n = 4 \).

 

Her er \( \large h = \frac{2-0}{4} = 0{,}5 \).

 

Funktionsværdierne er:

 

$$ \large f(0)=0, \quad f(0{,}5)=0{,}25, \quad f(1)=1, \quad f(1{,}5)=2{,}25, \quad f(2)=4 $$

 

Ved indsættelse i Simpsons formel får vi:

 

$$ \large A \approx \frac{0{,}5}{3}\,[0 + 4(0{,}25) + 2(1) + 4(2{,}25) + 4] = 2{,}67 $$

 

Det svarer præcist til det eksakte integral:

 

$$ \large \int_0^2 x^2\,dx = \frac{8}{3} = 2{,}67 $$

 

 

 

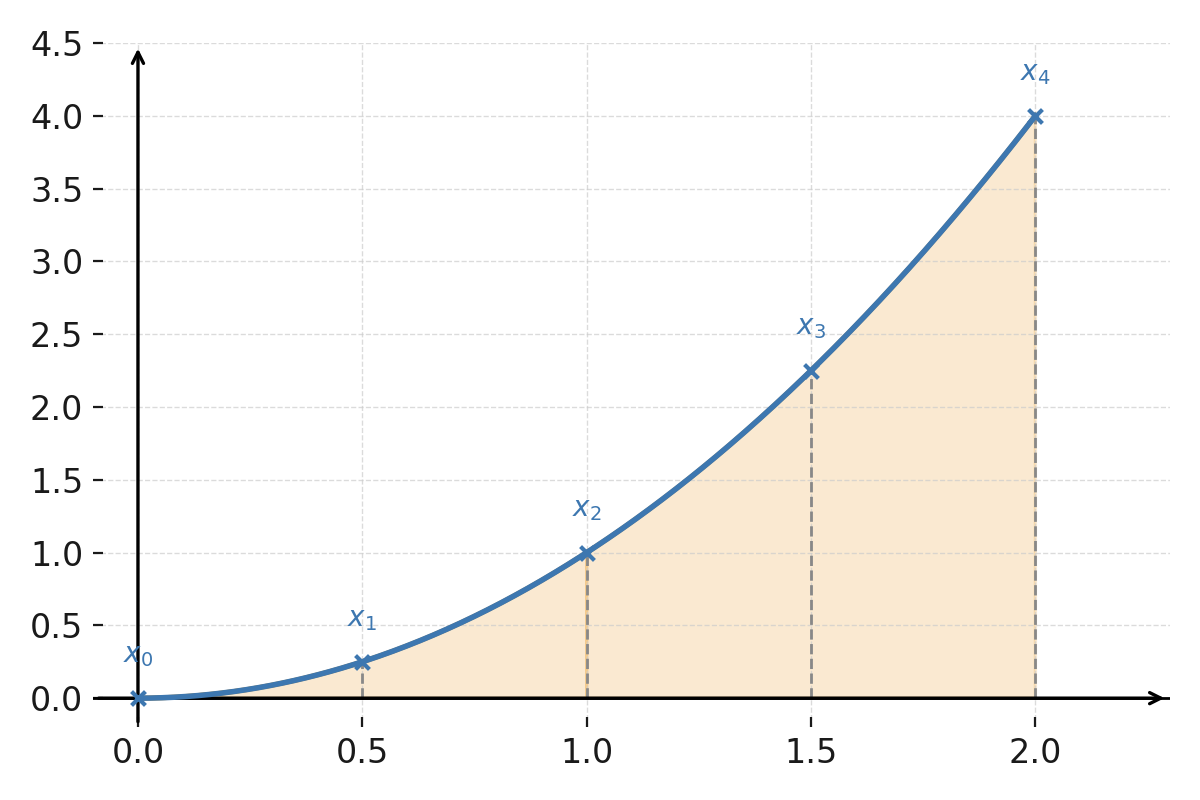
Funktionen \( \large f(x)=x^2 \).

Over hvert par af delintervaller er en parabel, som tilnærmer funktionen. Grænserne \( \large x_0, x_1, x_2, x_3, x_4 \) er markeret med grå stiplede linjer.

 

 

Bemærkninger

Simpsons regel giver en langt bedre nøjagtighed end trapezmetoden, fordi den tager højde for kurvens krumning. Den kan dog kun anvendes, når antallet af delintervaller \( \large n \) er lige. Ved kombination med flere parabler kaldes metoden også den sammensatte Simpsons regel.