Numerisk differentiation

Når man ikke har en analytisk formel for funktionen, kan man finde den afledte \( \large f'(x) \) ved at bruge numeriske metoder. Numerisk differentiation bygger på at tilnærme tangenthældningen ud fra diskrete punkter i stedet for at bruge den eksakte grænseværdi.

 

 

Idéen bag metoden

Den afledte i et punkt beskriver funktionen lokalt som hældningen på tangenten. Hvis man kender funktionsværdierne i punkter, der ligger tæt på hinanden, kan man beregne en tilnærmet hældning mellem dem. Det gøres ved at bruge differenskvotienter.

 

 

Fremad-, bagud- og centraldifferens

Der findes tre grundlæggende formler til numerisk differentiation:

 

Fremad differens:

 

$$ \large f'(x) \approx \frac{f(x+h) - f(x)}{h} $$

 

Bagud differens:

 

$$ \large f'(x) \approx \frac{f(x) - f(x-h)}{h} $$

 

Central differens:

 

$$ \large f'(x) \approx \frac{f(x+h) - f(x-h)}{2h} $$

 

Den centrale differens giver som regel den bedste nøjagtighed, fordi den tager hensyn til punkter på begge sider af \( \large x \).

 

 

Eksempel

Antag at vi vil beregne den afledte af \( \large f(x) = x^2 \) i punktet \( \large x = 1 \) med \( \large h = 0{,}1 \).

 

De nødvendige funktionsværdier er:

 

$$ \large f(1+h) = f(1{,}1) = 1{,}21, \quad f(1-h) = f(0{,}9) = 0{,}81 $$

 

Indsættes i formlerne:

 

$$ \large f'_{\text{fremad}}(1) = \frac{1{,}21 - 1}{0{,}1} = 2{,}1 $$

$$ \large f'_{\text{bagud}}(1) = \frac{1 - 0{,}81}{0{,}1} = 1{,}9 $$

$$ \large f'_{\text{central}}(1) = \frac{1{,}21 - 0{,}81}{0{,}2} = 2{,}0 $$

 

Den sande værdi af \( \large f'(x) = 2x \) er \( \large 2 \), så den centrale differens giver det mest præcise resultat.

 

 

 

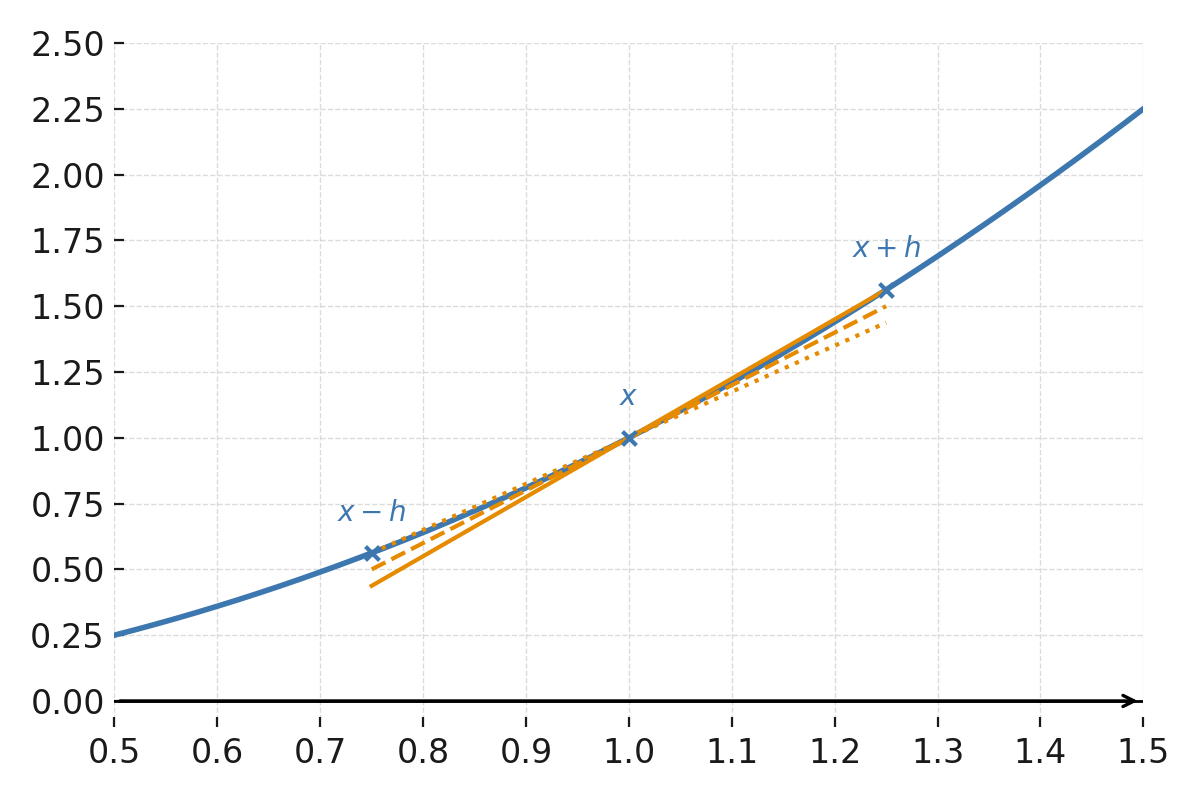
Funktionen \( \large f(x) = x^2 \) omkring punktet \( \large x=1 \).

De tre hældninger (fremad, bagud og central) viser forskellen mellem at bruge punkterne \( \large (x,f(x)) \), \( \large (x+h,f(x+h)) \) og \( \large (x-h,f(x-h)) \).

 

 

Bemærkninger

Nøjagtigheden afhænger af, hvor lille \( \large h \) er. For stort \( \large h \) giver en dårlig tilnærmelse, mens for lille \( \large h \) kan give afrundingsfejl. I praksis vælges \( \large h \) sådan, at differenskvotienten er stabil og giver en rimelig nøjagtighed.