Numeriske differentialligninger (Euler, Runge-Kutta)

Når en differentialligning ikke kan løses analytisk, kan man finde en tilnærmet løsning ved at bruge numeriske metoder. Disse metoder beregner funktionens værdier punkt for punkt ud fra differentialligningen og en startbetingelse. To af de mest brugte er Eulers metode og Runge–Kutta-metoden.

 

 

Idéen bag numeriske differentialligninger

En simpel ordinær differentialligning har formen:

 

$$ \large y' = f(x,y) $$

 

Hvis man kender en startværdi \( \large y(x_0) = y_0 \), kan man bruge \( \large f(x,y) \) til at beregne, hvordan \( y \) ændrer sig, når \( x \) øges en lille smule. Denne proces gentages trinvist, så man gradvist bygger en numerisk løsning.

 

 

Eulers metode

Eulers metode er den enkleste numeriske løsning. Den bruger differentialligningen direkte til at beregne den næste værdi som:

 

$$ \large y_{n+1} = y_n + h \cdot f(x_n, y_n) $$

 

Her er \( \large h \) trinstørrelsen. Ved at gentage for mange små trin kan man tegne en tilnærmet kurve for \( y(x) \).

 

 

Eksempel på Eulers metode

Vi vil løse \( \large y' = y \) med startbetingelsen \( \large y(0) = 1 \) og \( \large h = 0{,}5 \).

 

For hvert trin gælder:

 

$$ \large y_{n+1} = y_n + 0{,}5 \cdot y_n = 1{,}5y_n $$

 

Efter fire trin fås:

 

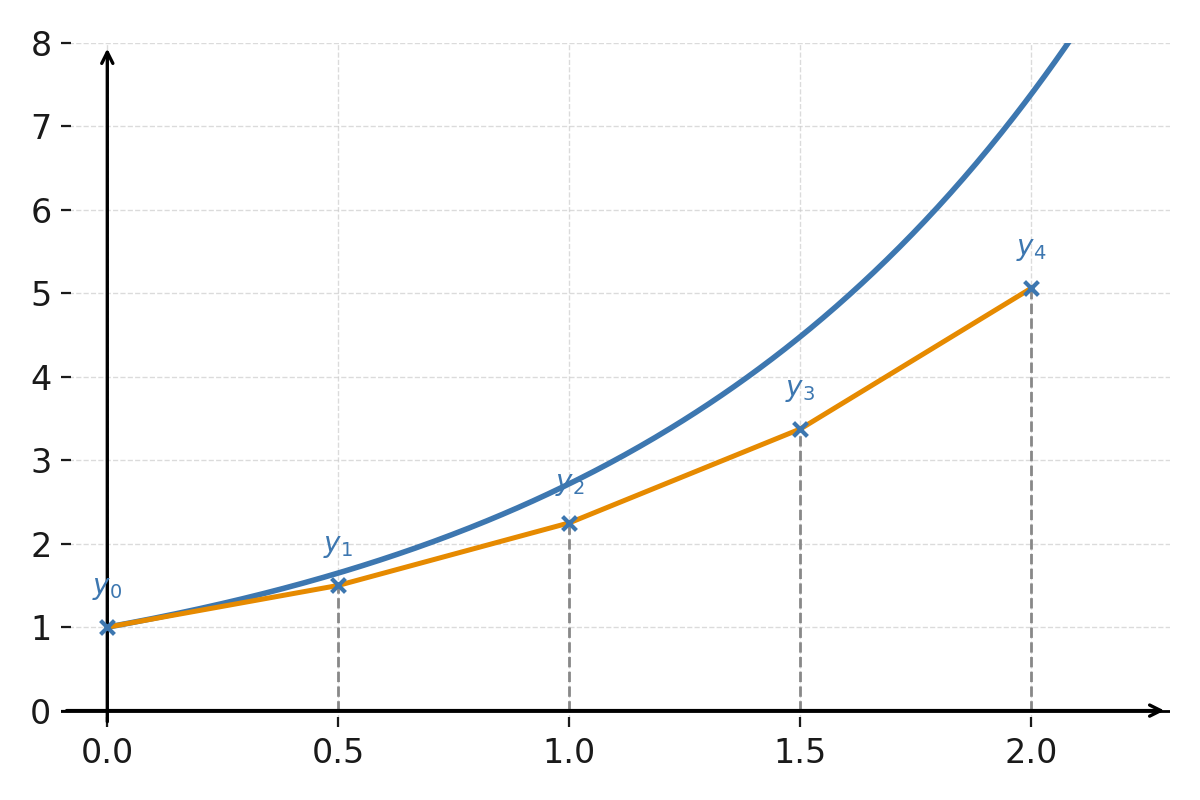
$$ \large y_1 = 1{,}5, \quad y_2 = 2{,}25, \quad y_3 = 3{,}375, \quad y_4 = 5{,}0625 $$

 

Den eksakte løsning er \( \large y = e^x \), og ved \( \large x=2 \) får vi \( \large e^2 \approx 7{,}389 \). Eulers metode undervurderer altså den rigtige kurve, fordi hvert trin bruger en ret linje i stedet for den krumme funktion.

 

 

 

 

Runge–Kutta-metoden (4. orden)

For bedre nøjagtighed kan man bruge Runge–Kutta af 4. orden (ofte kaldet RK4). Den tager gennemsnittet af fire hældninger i stedet for kun én:

 

$$ 
\large 
\begin{aligned}
k_1 &= f(x_n, y_n) \\[8pt]
k_2 &= f\!\left(x_n + \frac{h}{2},\, y_n + \frac{h}{2}k_1\right) \\[8pt]
k_3 &= f\!\left(x_n + \frac{h}{2},\, y_n + \frac{h}{2}k_2\right) \\[8pt]
k_4 &= f\!\left(x_n + h,\, y_n + h k_3\right) \\[8pt]
y_{n+1} &= y_n + \frac{h}{6}\!\left(k_1 + 2k_2 + 2k_3 + k_4\right)
\end{aligned}
$$

 

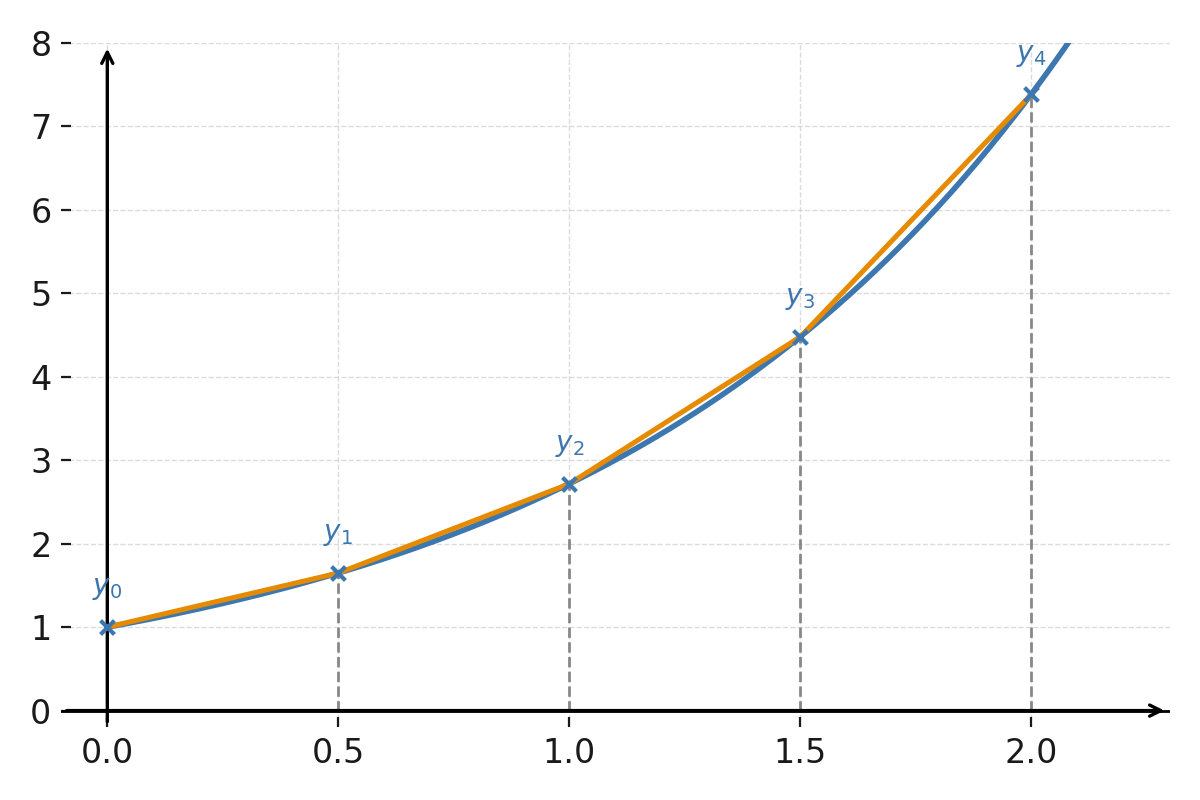
RK4 er meget mere nøjagtig end Eulers metode, selv med få trin, og bruges derfor ofte i praksis.

 

 

 

 

Bemærkninger

Numeriske differentialligninger er et af de vigtigste værktøjer i anvendt matematik, fysik og teknik. De bruges til at simulere systemer, hvor man kender ændringsraten, men ikke kan finde en lukket formel for selve funktionen.