Newton-Raphson metoden

Newton-Raphson-metoden er en hurtig numerisk metode til at finde rødder i en funktion, dvs. punkter hvor $ \large f(x) = 0 $. Metoden bruger både funktionsværdien og den afledte af funktionen til at forbedre gæt for rodens position.

Idéen bag metoden

Udgangspunktet er et startgæt $ \large x_0 $. I punktet $ \large (x_0, f(x_0)) $ tegnes tangenten til kurven. Skæringspunktet mellem denne tangent og x-aksen bruges som nyt gæt $ \large x_1 $. Processen gentages, indtil forskellen mellem to på hinanden følgende gæt er mindre end en valgt tolerance $ \large \varepsilon $.

Formel

$$ \large x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)} $$

Trinvis fremgangsmåde

Vælg et startpunkt $ \large x_0 $.
Beregn $ \large f(x_0) $ og $ \large f'(x_0) $.
Brug formlen til at finde $ \large x_1 $.
Gentag, indtil $ \large |x_{n+1} - x_n| < \varepsilon $.

Eksempel

Vi vil finde roden til $ \large f(x) = x^3 - x - 2 $, som vi tidligere løste med halveringsmetoden.

Den afledte er $ \large f'(x) = 3x^2 - 1 $.

Vi vælger et startgæt $ \large x_0 = 1{,}5 $.

$$ \large f(1{,}5) = (1{,}5)^3 - 1{,}5 - 2$$

$$ \large f(1{,}5) = -0{,}125 $$

$$ \large f'(1{,}5) = 3(1{,}5)^2 - 1 $$

$$ \large f'(1{,}5) = 5{,}75 $$

$$ \large x_1 = 1{,}5 - \frac{-0{,}125}{5{,}75} $$

$$ \large x_1 = 1{,}5217 $$

Efter få iterationer konvergerer metoden hurtigt mod roden $ \large x \approx 1{,}521 $.

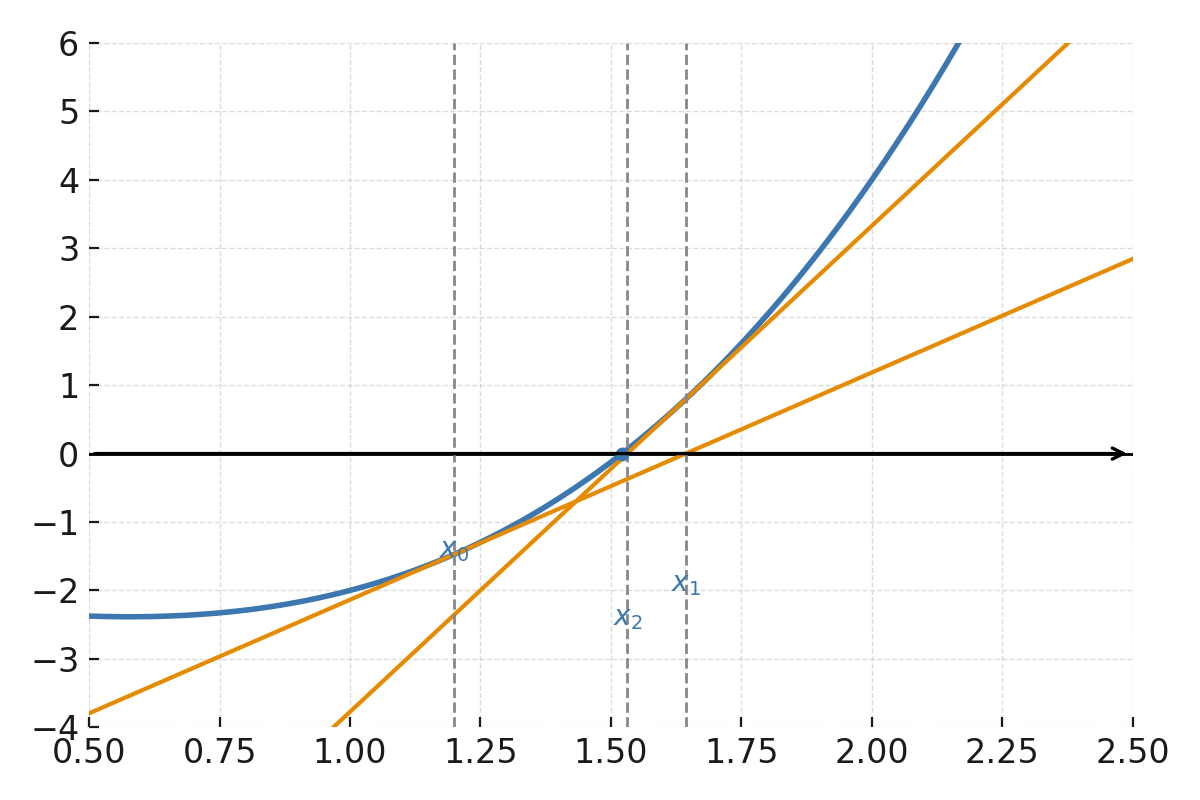
Newton-Raphson metoden

Funktionen $ \large f(x) = x^3 - x - 2 $ . Startgættet $ \large x_0 $ markeres på x-aksen, og tangenten i $ \large x_0 $ tegnes som en lijne, der skærer x-aksen i $ \large x_1 $. Dernæst vises tangent i $ \large x_1 $, som skærer x-aksen endnu tættere på roden. Figuren illustrerer den iterative forbedring.

Bemærkninger

Newton-Raphson-metoden konvergerer meget hurtigere end halveringsmetoden, men den kræver, at den afledte funktion $ \large f'(x) $ kan beregnes, og at startgættet ligger tæt på den faktiske rod. Hvis tangenten er næsten vandret (dvs. $ \large f'(x) \approx 0 $), kan metoden fejle eller springe forbi roden.