Halveringsmetoden (bisection)

Halveringsmetoden er en simpel numerisk metode til at finde en rod i en kontinuert funktion, altså et punkt hvor $ \large f(x) = 0 $.

Metoden bygger på sætningen om mellemværdi, som siger, at hvis $ \large f(a) $ og $ \large f(b) $ har modsat fortegn, må der eksistere mindst én rod i intervallet $ \large [a,b] $.

Idéen bag metoden

Intervallet deles gentagne gange i to halvdele. Ved hvert trin undersøges, i hvilken halvdel funktionen skifter fortegn. Denne halvdel vælges som det nye interval, og processen gentages, indtil rodens position er kendt med ønsket nøjagtighed.

Trinvis fremgangsmåde

Vælg et startinterval $ \large [a,b] $, hvor $ \large f(a) $ og $ \large f(b) $ har modsat fortegn.
Beregn midtpunktet $ \large m = \frac{a + b}{2} $.
Evaluer $ \large f(m) $.
Hvis $ \large f(m) = 0 $ (eller meget tæt på 0), er $ \large m $ roden.
Ellers: hvis $ \large f(a) $ og $ \large f(m) $ har modsat fortegn, sæt $ \large b = m $; ellers sæt $ \large a = m $.
Gentag trin 2–5, indtil intervallets længde er mindre end den valgte tolerance $ \large \varepsilon $.

Eksempel

Vi vil finde roden til funktionen $ \large f(x) = x^3 - x - 2 $.

Vi ser, at $ \large f(1) = -2 $ og $ \large f(2) = 4 $, altså skifter funktionen fortegn i intervallet $ \large [1,2] $.

$$ \large m_1 = \frac{1 + 2}{2} = 1{,}5 $$

$$ \large f(1{,}5) = (1{,}5)^3 - 1{,}5 - 2 $$

$$ \large f(1{,}5) = -0{,}125 $$

Fordi $ \large f(1{,}5) $ og $ \large f(2) $ har modsat fortegn, vælges nyt interval $ \large [1{,}5, 2] $.

$$ \large m_2 = \frac{1{,}5 + 2}{2} = 1{,}75 $$

$$ \large f(1{,}75) = (1{,}75)^3 - 1{,}75 - 2 $$

$$ \large f(1{,}75) = 1{,}609 - 3{,}75 $$

$$ \large f(1{,}75) = -0{,}109 $$

Processen gentages, indtil $ \large a $ og $ \large b $ ligger så tæt, at man kan aflæse roden som $ \large x \approx 1{,}521 $.

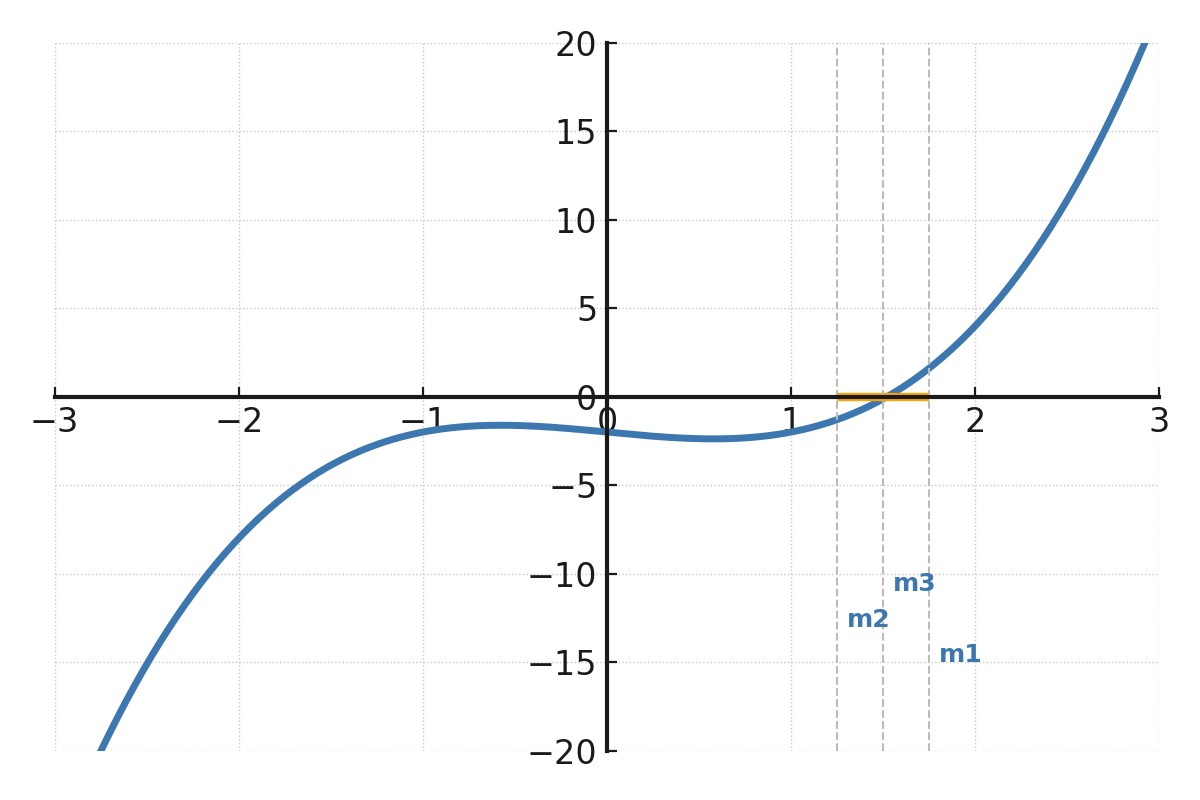
Halveringsmetoden

Funktionen $ \large f(x) = x^3 - x - 2 $, hvor intervallet $ \large [1,2] $ er markeret med en linje på x-aksen.

Midtpunkterne $ \large m_1, m_2, m_3 $ ses som lodrette streger, der gradvist nærmer sig rodens position, hvor grafen krydser x-aksen.

Bemærk

Halveringsmetoden er meget robust, fordi den altid konvergerer, hvis funktionen er kontinuert og har fortegnsskift. Ulempen er, at den konvergerer langsomt sammenlignet med mere avancerede metoder som Newton-Raphson.