Suma y resta

Al trabajar con vectores en el plano, se pueden sumar o restar. Esto se hace combinando las coordenadas de cada vector.

 

Definición

Para dos vectores \( \large \mathbf{u} = (x_1,y_1) \) y \( \large \mathbf{v} = (x_2,y_2) \), se cumple:

 

$$ \large \mathbf{u} + \mathbf{v} = (x_1 + x_2,\; y_1 + y_2) $$

 

$$ \large \mathbf{u} - \mathbf{v} = (x_1 - x_2,\; y_1 - y_2) $$

 

 

Ejemplo

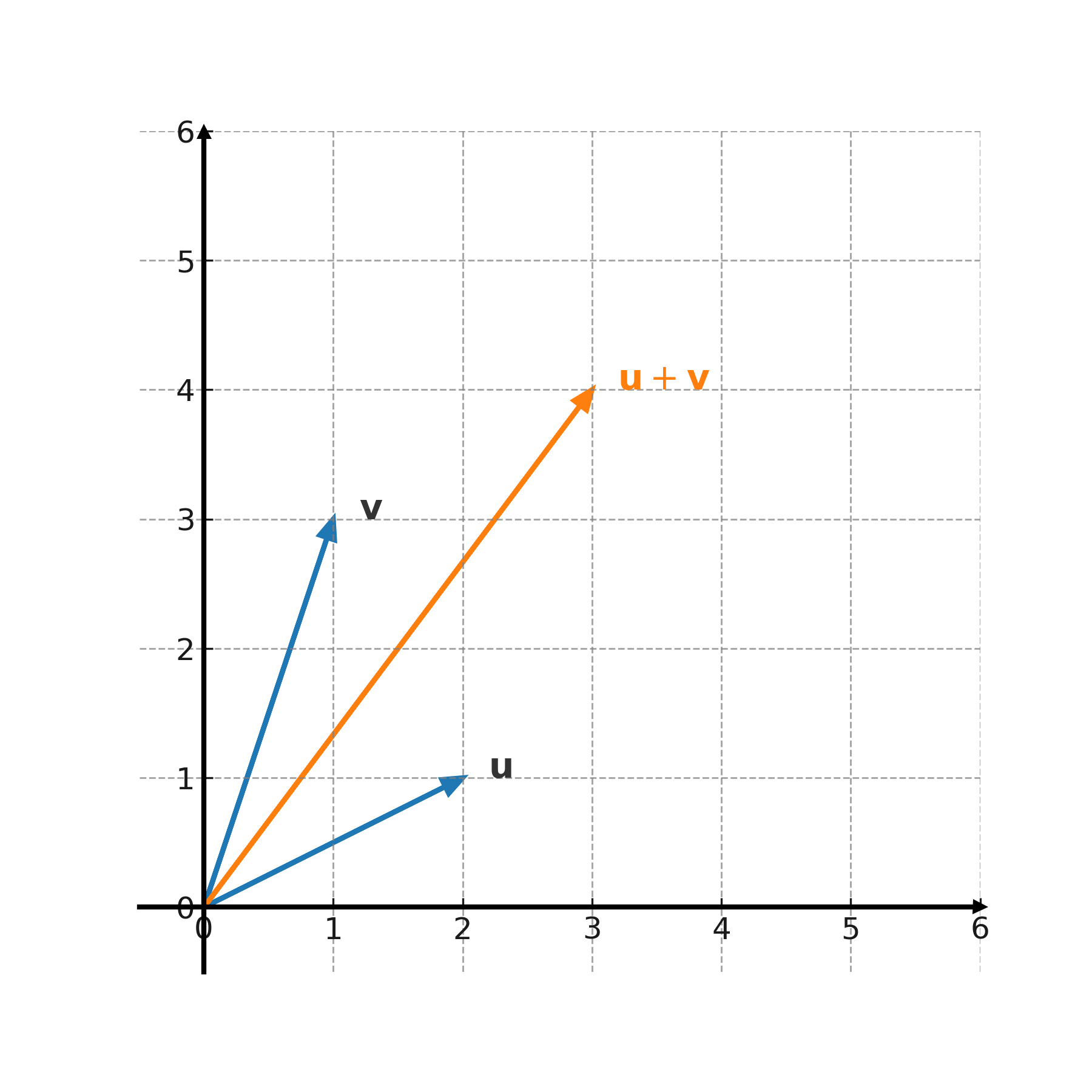
Queremos calcular la suma y la diferencia de los vectores \( \large \mathbf{u} = (2,1) \) y \( \large \mathbf{v} = (1,3) \).

 

La suma es:

 

$$ \large (2,1) + (1,3) = (2+1,\; 1+3) = (3,4) $$

 

 

La diferencia es:

 

$$ \large (2,1) - (1,3) = (2-1,\; 1-3) = (1,-2) $$

 

 

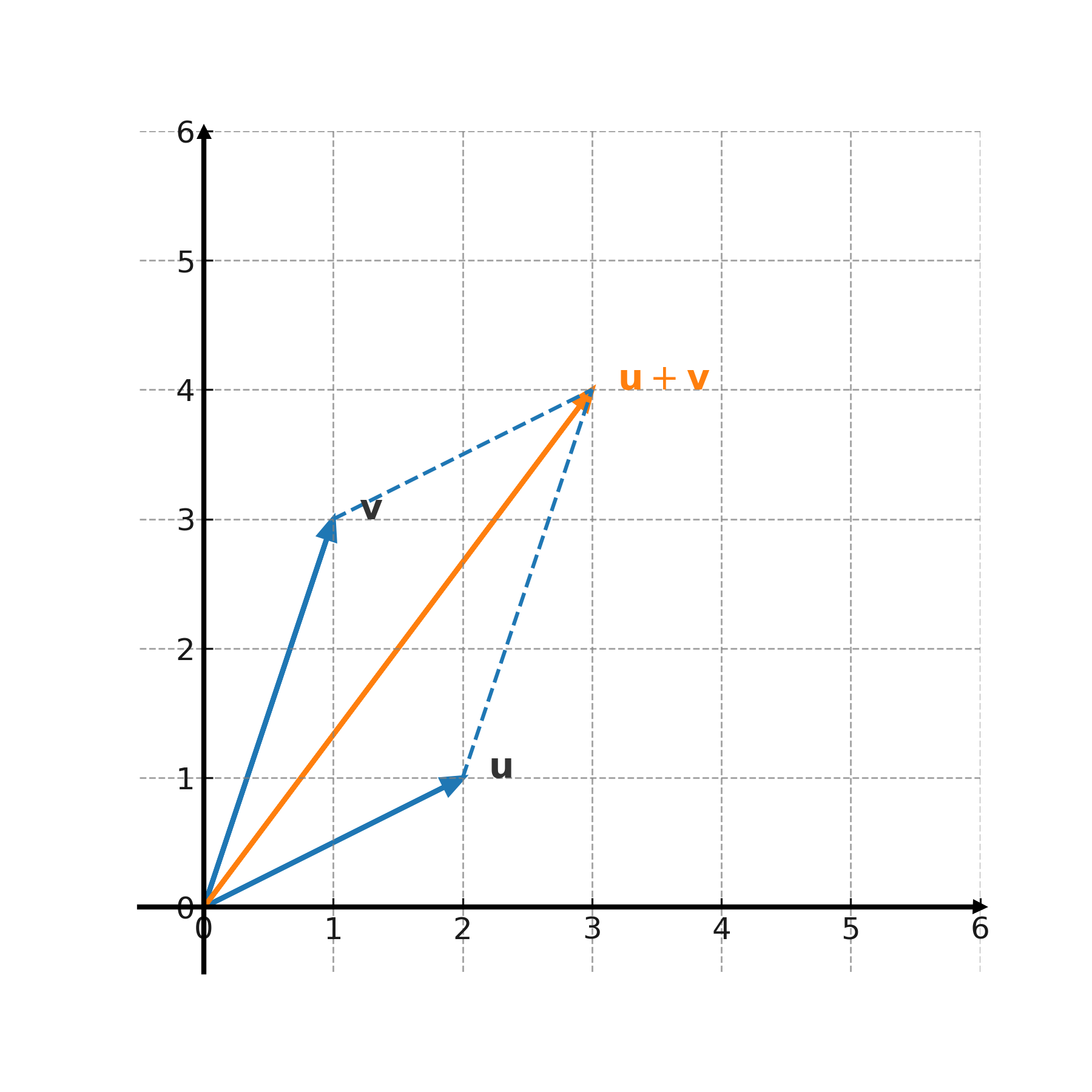
Interpretación geométrica

La suma puede mostrarse gráficamente con el método del paralelogramo: se colocan los vectores cola con cola y se dibujan dos copias para formar un paralelogramo. La diagonal representa la suma.

 

 

La resta puede verse como la suma del vector opuesto. Por ejemplo, \( \large \mathbf{u} - \mathbf{v} = \mathbf{u} + (-\mathbf{v}) \).

 

 

Aplicación

En física, la adición de vectores se utiliza para determinar la fuerza total sobre un cuerpo. Si una caja es tirada en una dirección por una fuerza y en otra dirección por otra fuerza, el movimiento resultante está dado por la suma de los dos vectores de fuerza.