Longitud y vectores unitarios

La longitud de un vector describe cuán grande es el vector, mientras que un vector unitario es un vector con longitud 1 en la misma dirección que el original.

 

Longitud

Para un vector \( \large \mathbf{v} = (x,y) \), la longitud se encuentra mediante:

 

$$ \large |\mathbf{v}| = \sqrt{x^2 + y^2} $$

 

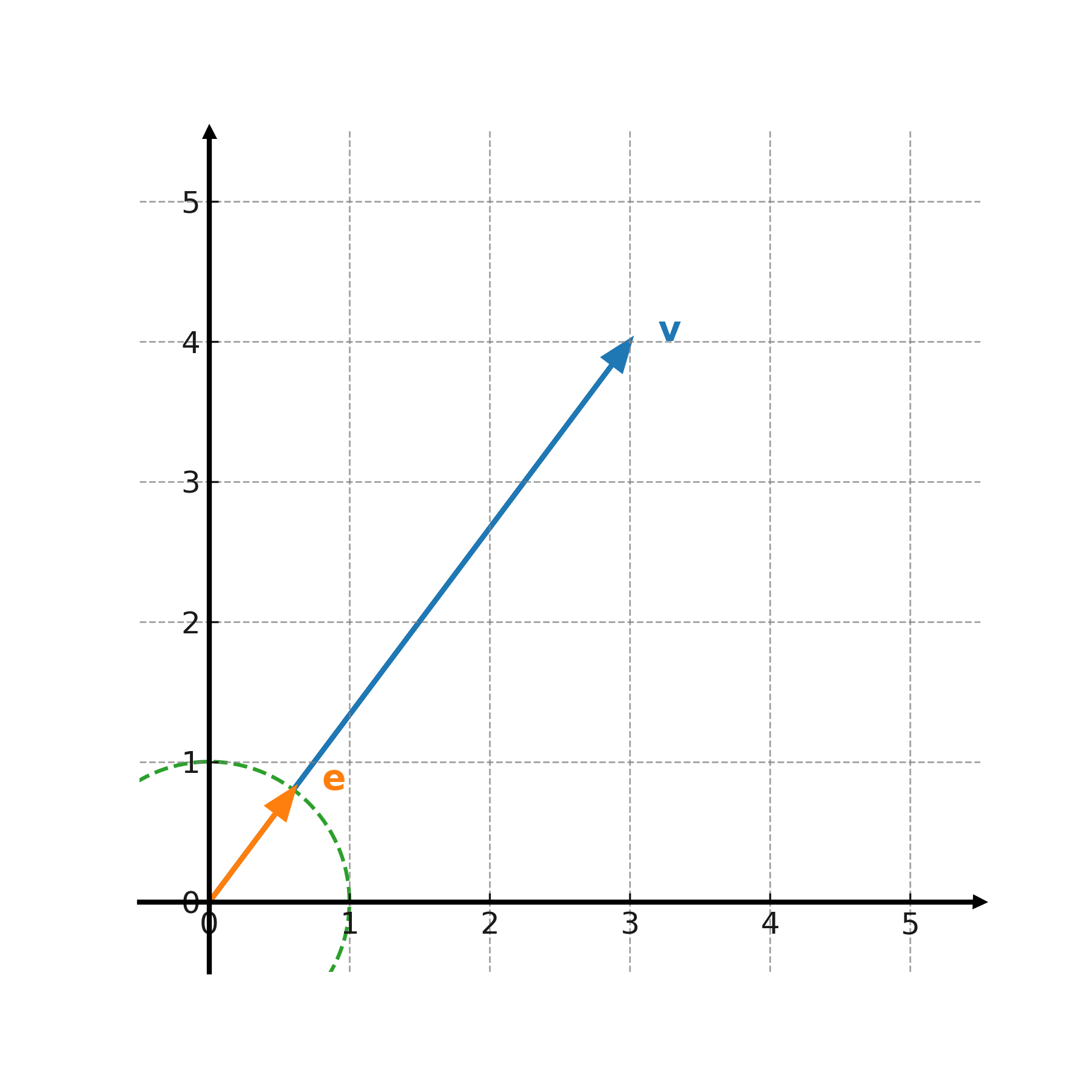
Ejemplo: El vector \( \large \mathbf{v} = (3,4) \) tiene la longitud

 

$$ \large |\mathbf{v}| = \sqrt{3^2 + 4^2} = 5 $$

 

Vector unitario

Un vector unitario se obtiene dividiendo un vector por su longitud:

 

$$ \large \mathbf{e} = \frac{1}{|\mathbf{v}|} \cdot \mathbf{v} $$

 

Ejemplo: Para \( \large \mathbf{v} = (3,4) \) se obtiene

 

$$ \large \mathbf{e} = \frac{1}{5} \cdot (3,4) = \left(\frac{3}{5}, \frac{4}{5}\right) $$

 

Nota: El vector nulo \( \large (0,0) \) no puede convertirse en vector unitario porque su longitud es 0 y no se puede dividir entre 0.

 

Los vectores unitarios más conocidos son los vectores unitarios estándar en el sistema de coordenadas:

 

$$ \large \mathbf{i} = (1,0), \quad \mathbf{j} = (0,1) $$

 

Interpretación geométrica

La longitud de un vector corresponde a la distancia desde el origen hasta el extremo del vector.

Un vector unitario es una flecha en la misma dirección, pero siempre con longitud 1.

 

 

Aplicación

Los vectores unitarios se utilizan para describir direcciones, sin que importe la magnitud. En física, se utilizan por ejemplo para indicar la dirección de una fuerza independientemente de su intensidad, y en matemáticas se utilizan para definir los ejes de los sistemas de coordenadas.