Producto escalar y ángulos

El producto escalar es una manera de combinar dos vectores que da un número. Se utiliza, entre otras cosas, para determinar el ángulo entre dos vectores y para decidir si son perpendiculares.

 

Definición

Para dos vectores \( \large \mathbf{u} = (x_1,y_1) \) y \( \large \mathbf{v} = (x_2,y_2) \), se cumple:

 

$$ \large \mathbf{u} \cdot \mathbf{v} = x_1 \cdot x_2 + y_1 \cdot y_2 $$

 

Además, el producto escalar puede escribirse como:

 

$$ \large \mathbf{u} \cdot \mathbf{v} = |\mathbf{u}| \cdot |\mathbf{v}| \cdot \cos(\theta) $$

 

donde \( \large \theta \) es el ángulo entre los vectores.

 

 

Ejemplos

Ejemplo 1:

 

$$ \large \mathbf{u} = (1,0), \; \mathbf{v} = (0,1) $$

$$ \large \mathbf{u} \cdot \mathbf{v} = 1 \cdot 0 + 0 \cdot 1 = 0 $$

 

Los vectores son ortogonales (perpendiculares), y el ángulo es \( \large 90^\circ \).

 

Ejemplo 2:

 

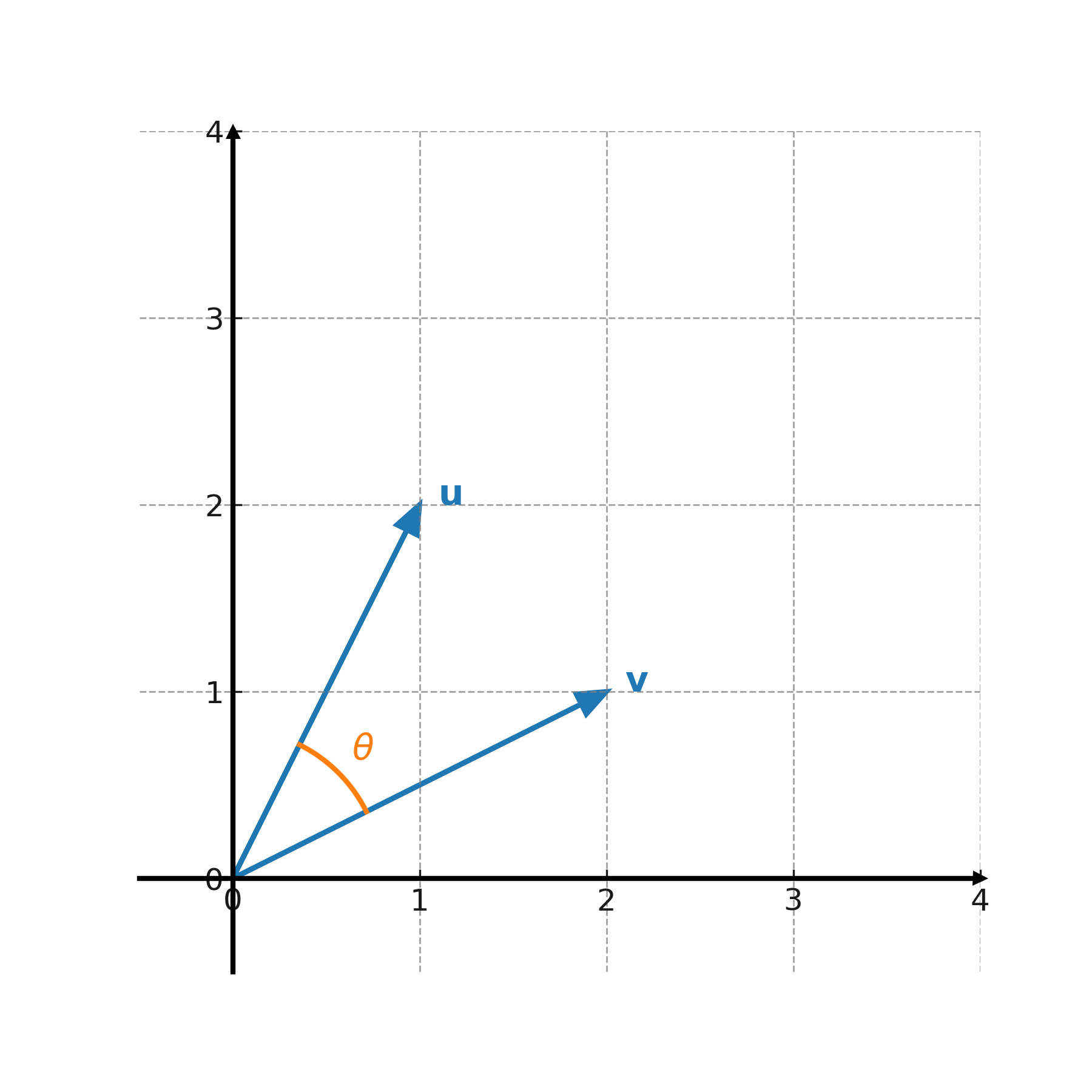
$$ \large \mathbf{u} = (1,2), \; \mathbf{v} = (2,1) $$

$$ \large \mathbf{u} \cdot \mathbf{v} = 1 \cdot 2 + 2 \cdot 1 = 4 $$

 

Las longitudes son \( \large |\mathbf{u}| = \sqrt{5}, \; |\mathbf{v}| = \sqrt{5} \). Así:

 

$$ \large \cos(\theta) = \frac{4}{\sqrt{5} \cdot \sqrt{5}} = \frac{4}{5} $$

 

El ángulo es por lo tanto:

 

$$ \large \theta = \cos^{-1}\left(\frac{4}{5}\right) \approx 36,9^\circ $$

 

 

Interpretación geométrica

El producto escalar mide cuánto de un vector apunta en la misma dirección que el otro. Si el ángulo es agudo, el producto es positivo. Si el ángulo es obtuso, el producto es negativo. Si el ángulo es recto, el producto es cero.

 

 

Aplicación

El producto escalar se utiliza en matemáticas y física para determinar ángulos y para decidir si los vectores son perpendiculares. En física, también se utiliza para calcular la parte de una fuerza que actúa en una dirección específica.