Multiplicación por un escalar

Cuando se multiplica un vector por un número, cambia su longitud, pero se conserva la dirección si el número es positivo. Si el número es negativo, el vector se invierte en la dirección opuesta.

 

Definición

Para un vector \( \large \mathbf{v} = (x,y) \) y un número \( \large k \), se cumple:

 

$$ \large k \cdot (x,y) = (k \cdot x,\; k \cdot y) $$

 

Ejemplos

Consideramos el vector \( \large \mathbf{v} = (2,1) \).

 

Cuando \( \large k = 2 \):

$$ \large 2 \cdot (2,1) = (4,2) $$

 

Cuando \( \large k = -1 \):

$$ \large -1 \cdot (2,1) = (-2,-1) $$

 

Cuando \( \large k = \frac{1}{2} \):

$$ \large \frac{1}{2} \cdot (2,1) = (1,\; \frac{1}{2}) $$

 

Cuando \( \large k = 0 \):

$$ \large 0 \cdot (2,1) = (0,0) $$

 

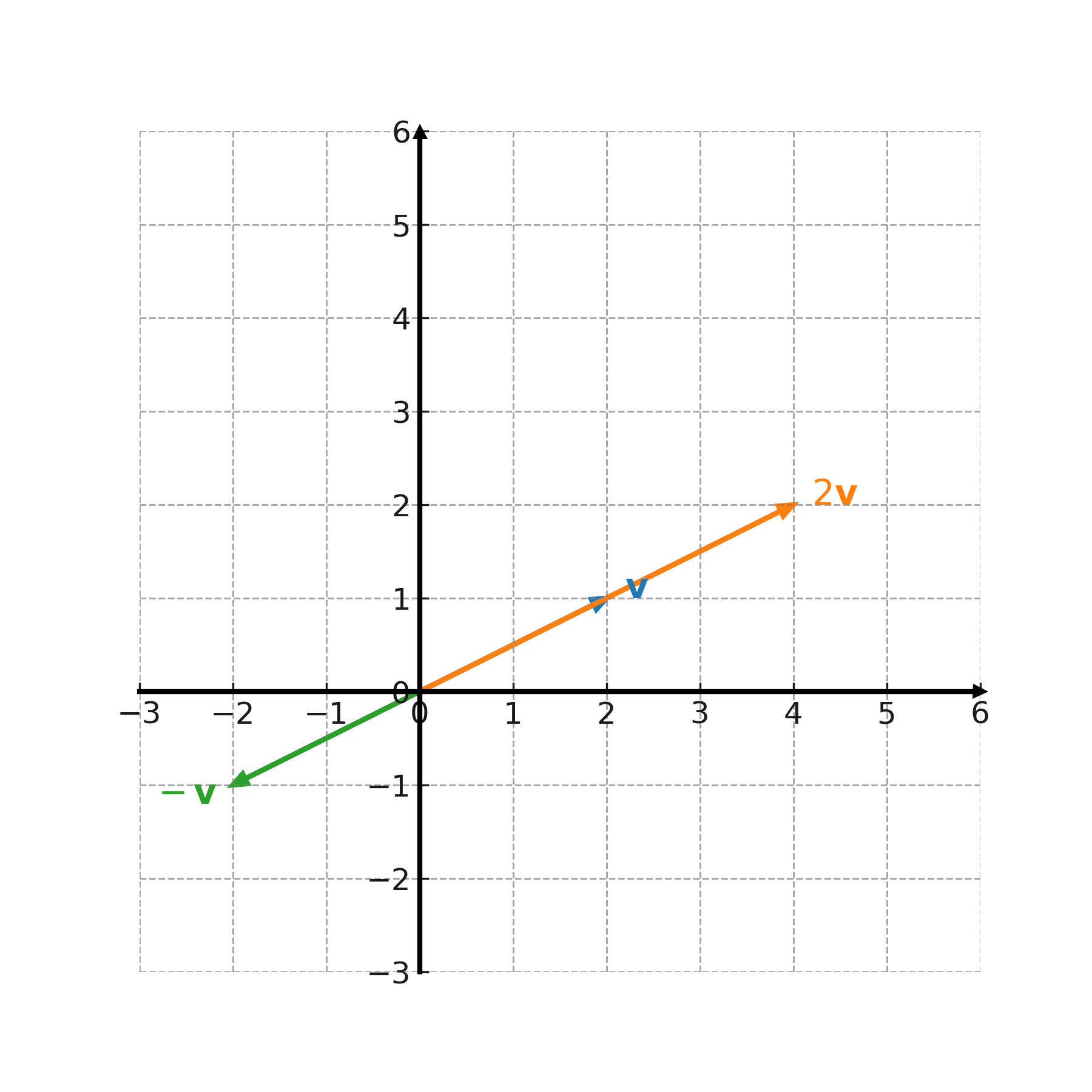
Interpretación geométrica

La multiplicación por un número estira o encoge el vector. Para números positivos, se conserva la dirección; para números negativos, la dirección se invierte. Cuando el número está entre 0 y 1, el vector se hace más corto, y cuando el número es 0, se obtiene el vector nulo.

 

 

Aplicación

La multiplicación por números se utiliza para cambiar la magnitud de un movimiento o de una fuerza. En física, esto corresponde a cambiar la intensidad de una fuerza sin cambiar su dirección.

 

En matemáticas, la multiplicación por parámetros se utiliza para describir rectas y curvas, por ejemplo \( \large (x,y) = (x_0,y_0) + t \cdot \mathbf{r} \), donde \( \large t \) es un número y \( \large \mathbf{r} \) un vector de dirección.