Área con vectores

El área de una figura puede calcularse utilizando vectores. En particular, los paralelogramos y triángulos pueden expresarse con una fórmula sencilla cuando se describen mediante dos vectores.

 

 

Área de paralelogramo y triángulo

Para dos vectores \( \large \mathbf{u} \) y \( \large \mathbf{v} \) en el plano, el área del paralelogramo que forman es:

 

$$ \large A = |\mathbf{u}| \cdot |\mathbf{v}| \cdot \sin(\theta) $$

 

donde \( \large \theta \) es el ángulo entre los vectores. La fórmula proviene de calcular base por altura, donde la altura se obtiene como la proyección de un vector sobre una dirección perpendicular al otro.

 

Otro método es usar el determinante:

 

$$ \large A = \left| \det \begin{pmatrix} x_1 & x_2 \\ y_1 & y_2 \end{pmatrix} \right| $$

 

si \( \large \mathbf{u} = (x_1,y_1) \) y \( \large \mathbf{v} = (x_2,y_2) \).

 

 

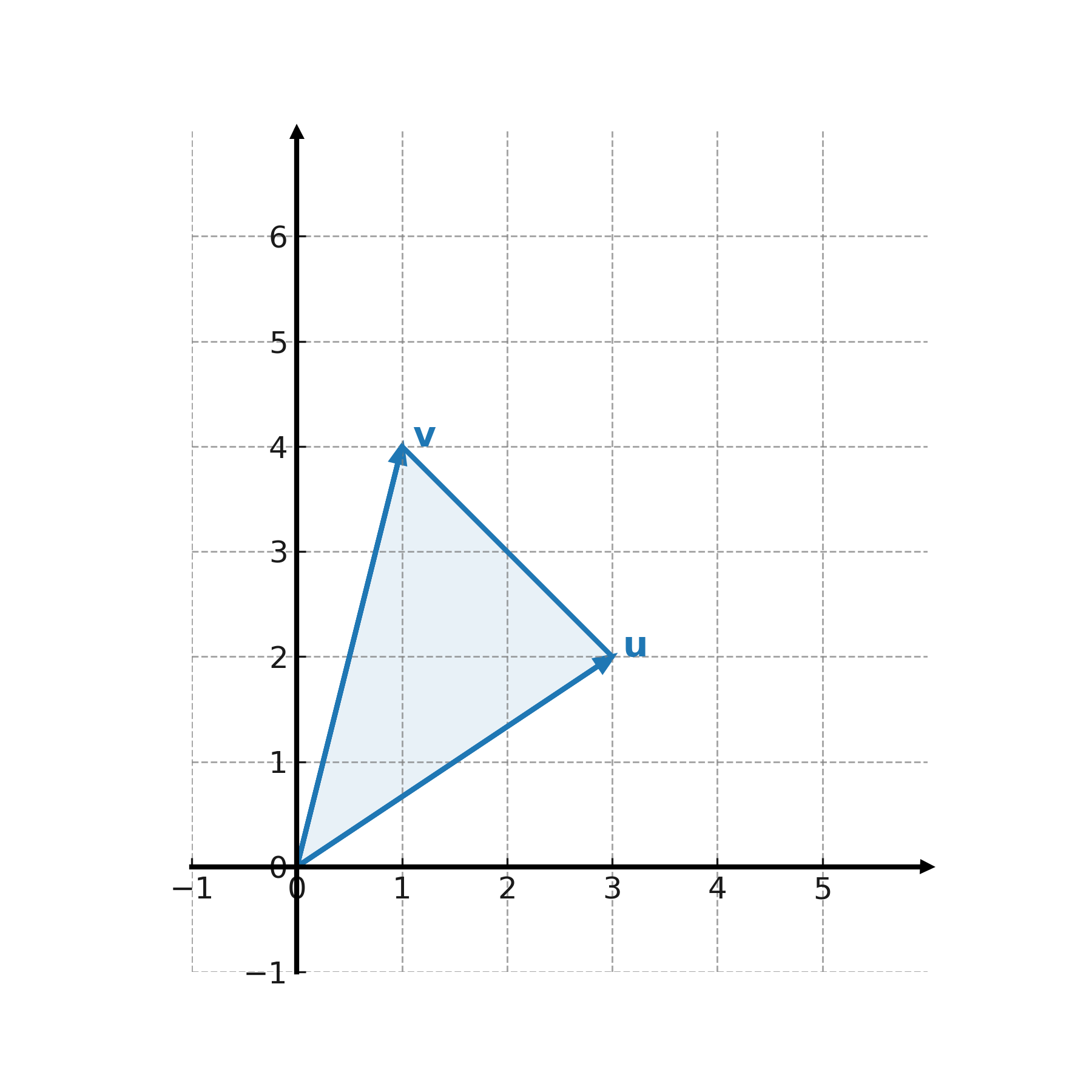
Ejemplo

Tomamos \( \large \mathbf{u} = (3,2) \) y \( \large \mathbf{v} = (1,4) \).

 

$$ \large A = \left| \det \begin{pmatrix} 3 & 1 \\ 2 & 4 \end{pmatrix} \right| = |3 \cdot 4 - 2 \cdot 1| = |10| = 10 $$

 

El área del paralelogramo es 10. 

El área del triángulo definido por los mismos dos vectores es la mitad, es decir \( \large 5 \).

 

 

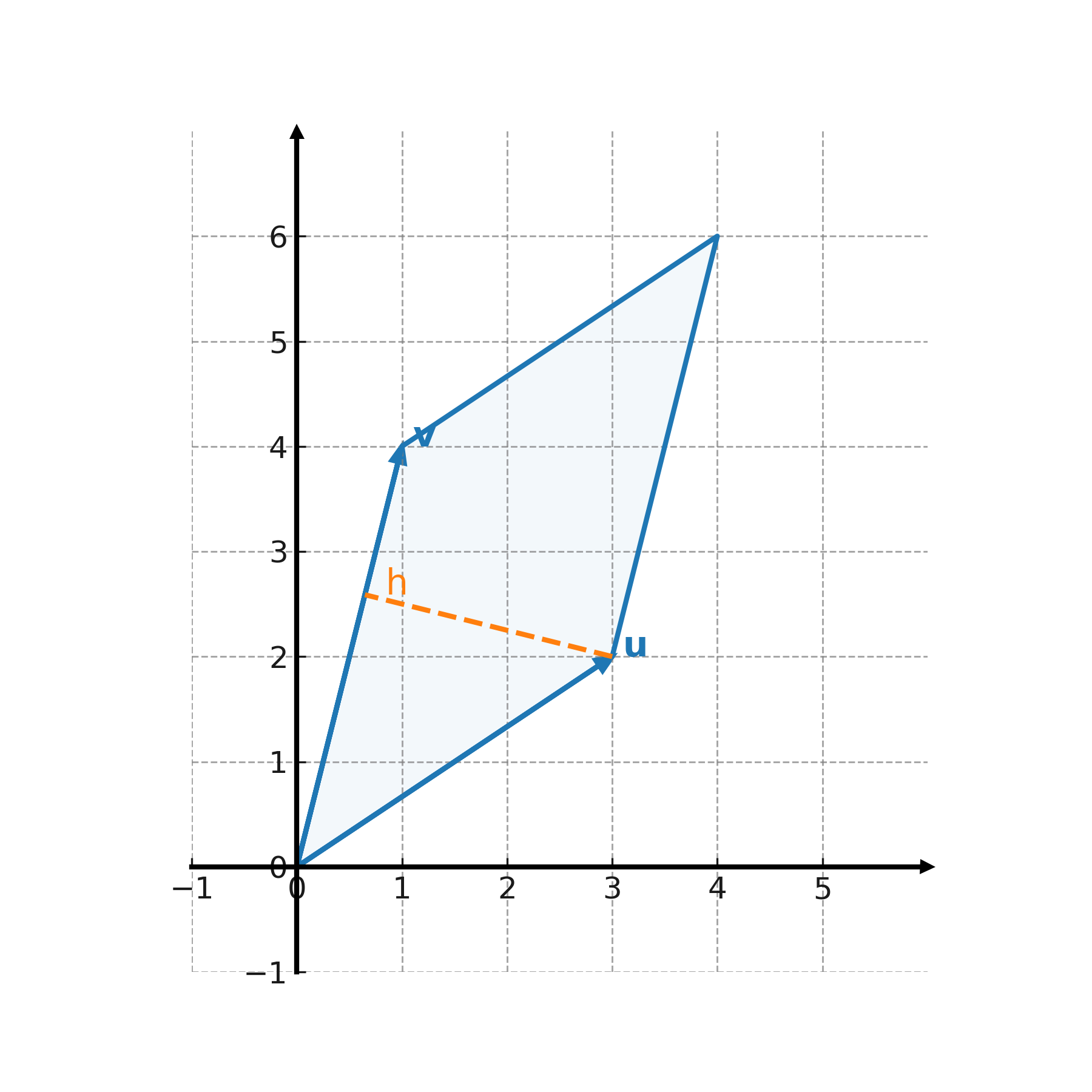
Interpretación geométrica

Lo más importante a notar es que el área puede calcularse como base por altura, y que la altura puede encontrarse utilizando la proyección. Así, el concepto de proyección está estrechamente relacionado con el cálculo de áreas.

 

 

Aplicación

Las fórmulas vectoriales para áreas se utilizan tanto en geometría como en álgebra lineal. Proporcionan un método sencillo para calcular áreas en sistemas de coordenadas y constituyen la base de temas posteriores como determinantes y volúmenes.