Trapezregel

Die Trapezmethode ist ein einfaches numerisches Verfahren zur Berechnung eines angenäherten Wertes eines bestimmten Integrals. Sie basiert auf der Idee, den Graphen einer Funktion durch gerade Linien zu ersetzen, sodass die Fläche unter der Kurve als Summe von Trapezen berechnet werden kann.

 

 

Idee der Methode

Wenn das genaue Integral \( \large \int_a^b f(x)\,dx \) nicht gefunden werden kann, kann das Intervall \( \large [a,b] \) in \( \large n \) kleinere Teilintervalle unterteilt werden. In jedem Teilintervall wird die Funktion durch eine Gerade zwischen den beiden Endpunkten ersetzt. Die Fläche unter dieser Geraden ist ein Trapez, das leicht zu berechnen ist.

 

 

Formel der Trapezmethode

Für ein Intervall, das in \( \large n \) gleich große Teile mit der Breite \( \large h = \frac{b-a}{n} \) unterteilt ist, gilt:

 

$$ \large \int_a^b f(x)\,dx \approx \frac{h}{2} \left[f(x_0) + 2f(x_1) + 2f(x_2) + \ldots + 2f(x_{n-1}) + f(x_n)\right] $$

 

 

Schrittweises Vorgehen

 

1. Teile das Intervall \( \large [a,b] \) in \( \large n \) gleich große Abschnitte.
2. Berechne \( \large h = \frac{b-a}{n} \).
3. Berechne die Funktionswerte \( \large f(x_0), f(x_1), \ldots, f(x_n) \).
4. Setze die Werte in die Trapezformel ein.

 

 

Beispiel

Wir berechnen die angenäherte Fläche unter der Funktion \( \large f(x) = x^2 \) im Intervall \( \large [0,2] \) mit 4 Trapezen.

 

Hier gilt \( \large a = 0 \), \( \large b = 2 \) und \( \large n = 4 \), also \( \large h = \frac{2-0}{4} = 0{,}5 \).

 

Die Funktionswerte sind:

 

$$ \large f(0)=0, \quad f(0{,}5)=0{,}25, \quad f(1)=1, \quad f(1{,}5)=2{,}25, \quad f(2)=4 $$

 

Die Trapezformel ergibt:

 

$$ \large A \approx \frac{0{,}5}{2}\,[0 + 2(0{,}25 + 1 + 2{,}25) + 4] = 2{,}75 $$

 

Das exakte Integral ist \( \large \int_0^2 x^2\,dx = \frac{8}{3} \approx 2{,}67 \), also liefert die Methode eine gute Näherung.

 

 

 

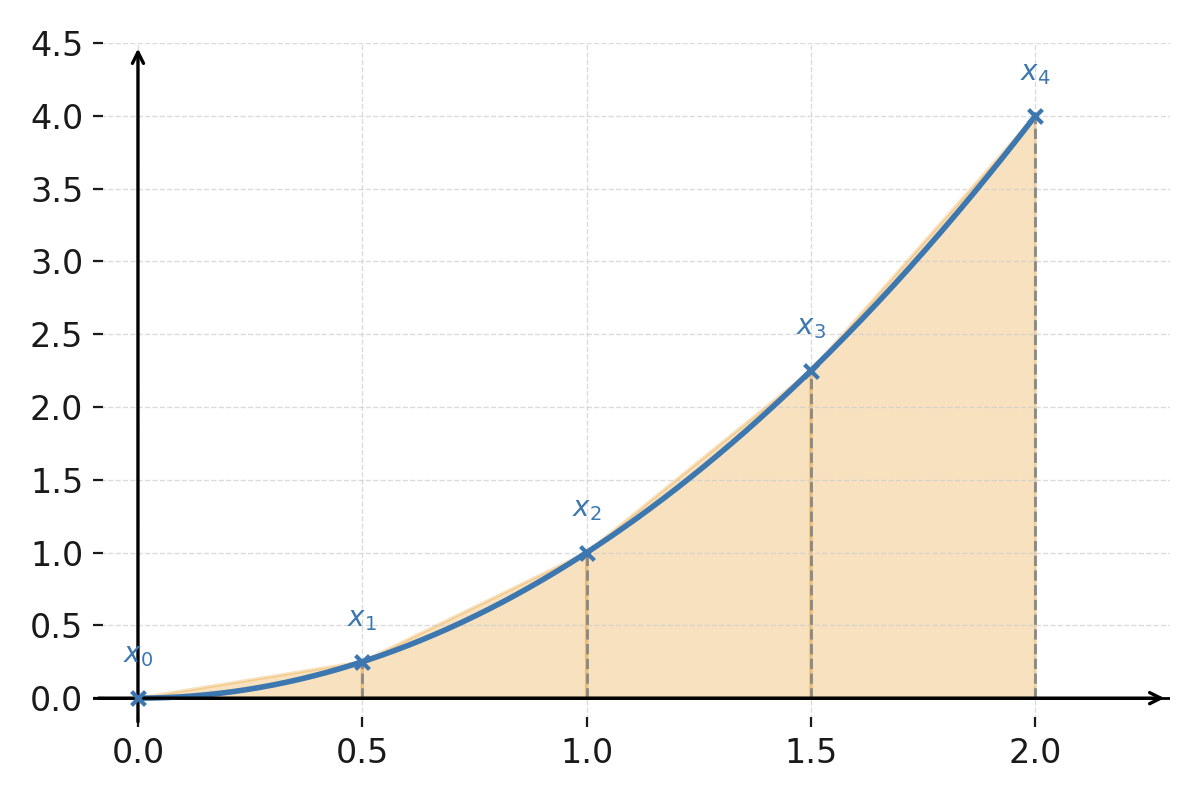
Die Funktion \( \large f(x) = x^2 \) im Intervall \( \large [0,2] \).

Die vier Teilintervalle sind durch vertikale gestrichelte Linien markiert, und die entsprechenden Trapeze sind zwischen der Kurve und der x-Achse dargestellt.

 

 

Hinweise

Die Trapezmethode ist leicht zu implementieren und liefert oft eine gute Genauigkeit, kann jedoch die Fläche unter- oder überschätzen, je nachdem, ob die Funktion konvex oder konkav ist. Die Genauigkeit kann verbessert werden, indem mehr Teilintervalle verwendet oder die Simpson-Regel angewendet wird.