Simpsons Regel

Die Simpson-Regel ist eine Verbesserung der Trapezmethode zur numerischen Berechnung eines bestimmten Integrals. Während die Trapezmethode die Funktion durch gerade Linien ersetzt, verwendet die Simpson-Regel Parabeln (quadratische Polynome), um die Kurve näherungsweise darzustellen. Dies liefert eine deutlich höhere Genauigkeit, selbst bei wenigen Teilintervallen.

 

 

Idee der Methode

Angenommen, wir wollen die Fläche unter der Funktion \( \large f(x) \) zwischen \( \large a \) und \( \large b \) berechnen. Das Intervall wird in eine gerade Anzahl von Teilintervallen unterteilt (zum Beispiel \( \large n = 4 \)). Über jedem Paar von Teilintervallen wird eine Parabel gezeichnet, die durch die drei Punkte \( \large (x_{2i}, f(x_{2i})) \), \( \large (x_{2i+1}, f(x_{2i+1})) \) und \( \large (x_{2i+2}, f(x_{2i+2})) \) verläuft. Die Summe der Flächen unter diesen Parabeln ergibt eine Näherung für das gesamte Integral.

 

 

Formel der Simpson-Regel

Wenn \( \large n \) gerade ist und die Teilbreite \( \large h = \frac{b-a}{n} \) beträgt, gilt:

 

$$ \large \int_a^b f(x)\,dx \approx \frac{h}{3}\,[f(x_0) + 4f(x_1) + 2f(x_2) + 4f(x_3) + \ldots + 4f(x_{n-1}) + f(x_n)] $$

 

Schrittweises Vorgehen

 

1. Teile das Intervall \( \large [a,b] \) in eine gerade Anzahl von Teilintervallen \( \large n \).
2. Berechne \( \large h = \frac{b-a}{n} \).
3. Berechne die Funktionswerte \( \large f(x_0), f(x_1), \ldots, f(x_n) \).
4. Setze die Werte in die Simpson-Formel ein.

 

 

Beispiel

Wir berechnen die angenäherte Fläche unter \( \large f(x) = x^2 \) im Intervall \( \large [0,2] \) mit \( \large n = 4 \).

 

Hier gilt \( \large h = \frac{2-0}{4} = 0{,}5 \).

 

Die Funktionswerte sind:

 

$$ \large f(0)=0, \quad f(0{,}5)=0{,}25, \quad f(1)=1, \quad f(1{,}5)=2{,}25, \quad f(2)=4 $$

 

Eingesetzt in die Simpson-Formel ergibt sich:

 

$$ \large A \approx \frac{0{,}5}{3}\,[0 + 4(0{,}25) + 2(1) + 4(2{,}25) + 4] = 2{,}67 $$

 

Dies entspricht genau dem exakten Integral:

 

$$ \large \int_0^2 x^2\,dx = \frac{8}{3} = 2{,}67 $$

 

 

 

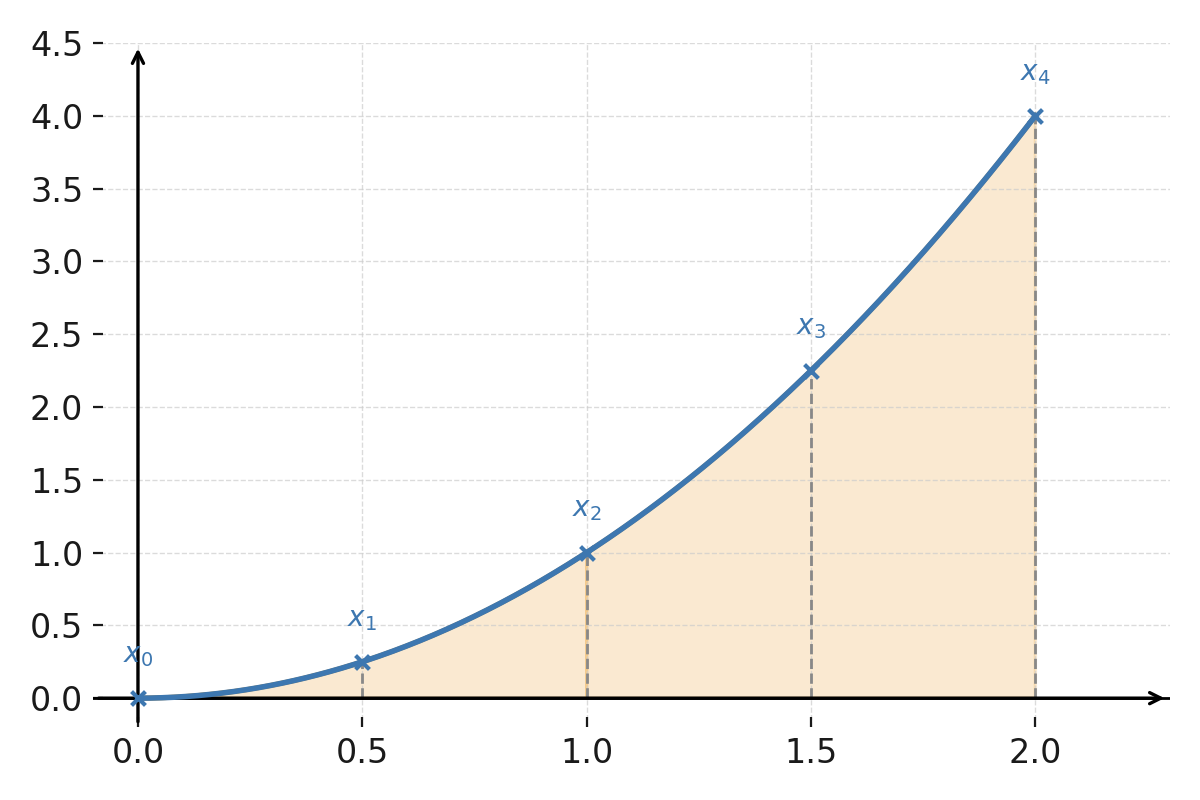
Die Funktion \( \large f(x)=x^2 \).

Über jedem Paar von Teilintervallen wird eine Parabel gezeichnet, die die Funktion annähert. Die Grenzen \( \large x_0, x_1, x_2, x_3, x_4 \) sind mit grauen gestrichelten Linien markiert.

 

 

Hinweise

Die Simpson-Regel liefert eine deutlich bessere Genauigkeit als die Trapezmethode, da sie die Krümmung der Funktion berücksichtigt. Sie kann jedoch nur angewendet werden, wenn die Anzahl der Teilintervalle \( \large n \) gerade ist. Wird sie mit mehreren Parabeln kombiniert, spricht man von der zusammengesetzten Simpson-Regel.