Bisektionsmethode

Das Bisektionsverfahren ist eine einfache numerische Methode, um eine Nullstelle in einer stetigen Funktion zu finden, also einen Punkt, an dem $ \large f(x) = 0 $ gilt.

Die Methode basiert auf dem Zwischenwertsatz, der besagt, dass, wenn $ \large f(a) $ und $ \large f(b) $ entgegengesetzte Vorzeichen haben, mindestens eine Nullstelle im Intervall $ \large [a,b] $ existieren muss.

Idee der Methode

Das Intervall wird wiederholt in zwei Hälften geteilt. In jedem Schritt wird bestimmt, in welcher Hälfte die Funktion das Vorzeichen wechselt. Diese Hälfte wird als neues Intervall gewählt, und der Prozess wird wiederholt, bis die Position der Nullstelle mit der gewünschten Genauigkeit bekannt ist.

Schrittweises Vorgehen

Wähle ein Startintervall $ \large [a,b] $, in dem $ \large f(a) $ und $ \large f(b) $ entgegengesetzte Vorzeichen haben.
Berechne den Mittelpunkt $ \large m = \frac{a + b}{2} $.
Berechne $ \large f(m) $.
Wenn $ \large f(m) = 0 $ (oder sehr nahe bei 0), ist $ \large m $ die Nullstelle.
Andernfalls: Wenn $ \large f(a) $ und $ \large f(m) $ entgegengesetzte Vorzeichen haben, setze $ \large b = m $; andernfalls setze $ \large a = m $.
Wiederhole die Schritte 2–5, bis die Intervalllänge kleiner als die gewählte Toleranz $ \large \varepsilon $ ist.

Beispiel

Wir wollen die Nullstelle der Funktion $ \large f(x) = x^3 - x - 2 $ finden.

Wir sehen, dass $ \large f(1) = -2 $ und $ \large f(2) = 4 $ gilt, also wechselt die Funktion im Intervall $ \large [1,2] $ das Vorzeichen.

$$ \large m_1 = \frac{1 + 2}{2} = 1{,}5 $$

$$ \large f(1{,}5) = (1{,}5)^3 - 1{,}5 - 2 $$

$$ \large f(1{,}5) = -0{,}125 $$

Da $ \large f(1{,}5) $ und $ \large f(2) $ entgegengesetzte Vorzeichen haben, wird ein neues Intervall $ \large [1{,}5, 2] $ gewählt.

$$ \large m_2 = \frac{1{,}5 + 2}{2} = 1{,}75 $$

$$ \large f(1{,}75) = (1{,}75)^3 - 1{,}75 - 2 $$

$$ \large f(1{,}75) = 1{,}609 - 3{,}75 $$

$$ \large f(1{,}75) = -0{,}109 $$

Der Prozess wird fortgesetzt, bis $ \large a $ und $ \large b $ so nah beieinander liegen, dass die Nullstelle als $ \large x \approx 1{,}521 $ abgelesen werden kann.

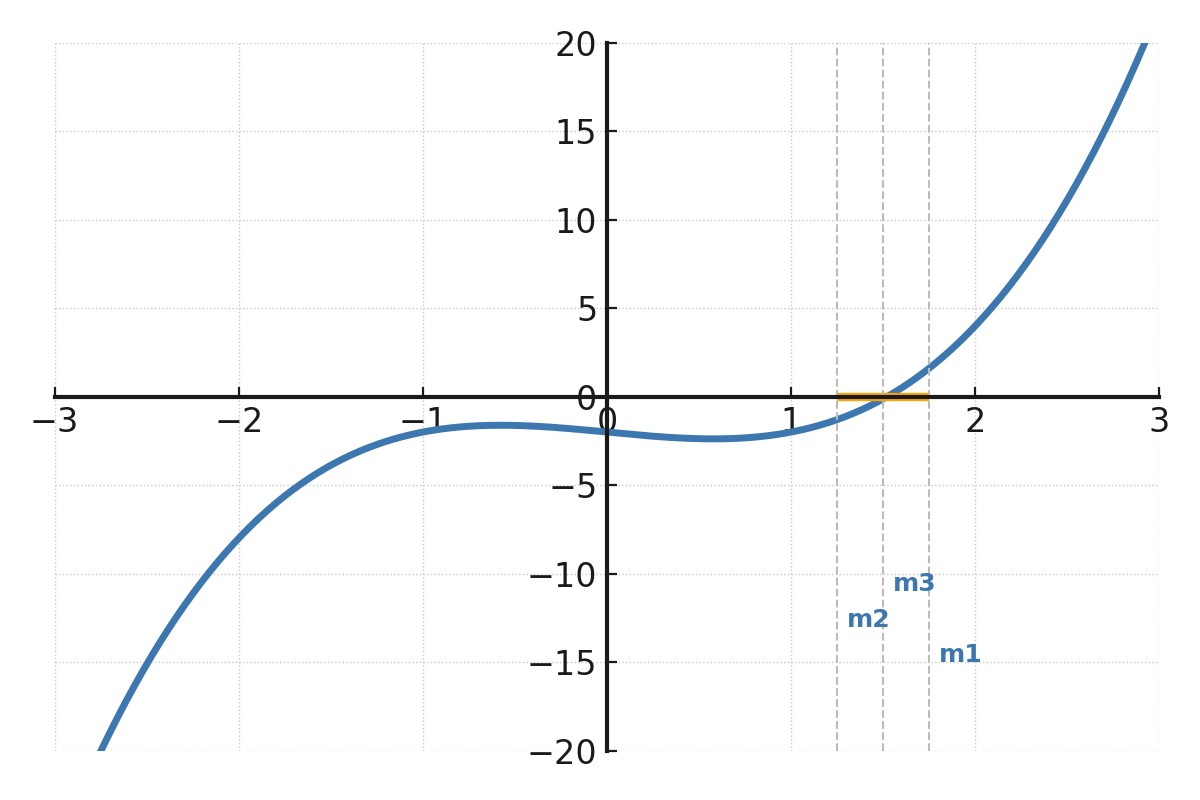
Bisektionsverfahren

Die Funktion $ \large f(x) = x^3 - x - 2 $, wobei das Intervall $ \large [1,2] $ als Linie auf der x-Achse markiert ist.

Die Mittelpunkte $ \large m_1, m_2, m_3 $ erscheinen als vertikale Linien, die sich schrittweise der Position der Nullstelle nähern, an der die Kurve die x-Achse schneidet.

Hinweis

Das Bisektionsverfahren ist sehr robust, da es immer konvergiert, wenn die Funktion stetig ist und ein Vorzeichenwechsel auftritt. Der Nachteil besteht darin, dass es im Vergleich zu fortgeschritteneren Methoden wie Newton-Raphson langsam konvergiert.