Numerische Differentiation
Wenn keine analytische Formel für die Funktion vorhanden ist, kann die Ableitung \( \large f'(x) \) mithilfe numerischer Methoden bestimmt werden. Die numerische Differentiation basiert darauf, die Steigung der Tangente aus diskreten Punkten zu approximieren, anstatt den exakten Grenzwert zu verwenden.
Idee der Methode
Die Ableitung in einem Punkt beschreibt die lokale Steigung der Tangente an die Funktion. Wenn die Funktionswerte an nahe beieinanderliegenden Punkten bekannt sind, kann eine angenäherte Steigung zwischen ihnen berechnet werden. Dies geschieht mithilfe von Differenzenquotienten.
Vorwärts-, Rückwärts- und Zentraldifferenz
Es gibt drei grundlegende Formeln für die numerische Differentiation:
Vorwärtsdifferenz:
$$ \large f'(x) \approx \frac{f(x+h) - f(x)}{h} $$
Rückwärtsdifferenz:
$$ \large f'(x) \approx \frac{f(x) - f(x-h)}{h} $$
Zentrales Differenzschema:
$$ \large f'(x) \approx \frac{f(x+h) - f(x-h)}{2h} $$
Die zentrale Differenz liefert in der Regel die beste Genauigkeit, da sie Punkte auf beiden Seiten von \( \large x \) berücksichtigt.
Beispiel
Angenommen, wir wollen die Ableitung von \( \large f(x) = x^2 \) an der Stelle \( \large x = 1 \) mit \( \large h = 0{,}1 \) berechnen.
Die benötigten Funktionswerte sind:
$$ \large f(1+h) = f(1{,}1) = 1{,}21, \quad f(1-h) = f(0{,}9) = 0{,}81 $$
Eingesetzt in die Formeln ergibt sich:
$$ \large f'_{\text{vorwärts}}(1) = \frac{1{,}21 - 1}{0{,}1} = 2{,}1 $$
$$ \large f'_{\text{rückwärts}}(1) = \frac{1 - 0{,}81}{0{,}1} = 1{,}9 $$
$$ \large f'_{\text{zentral}}(1) = \frac{1{,}21 - 0{,}81}{0{,}2} = 2{,}0 $$
Der wahre Wert von \( \large f'(x) = 2x \) ist \( \large 2 \), daher liefert die zentrale Differenz das genaueste Ergebnis.
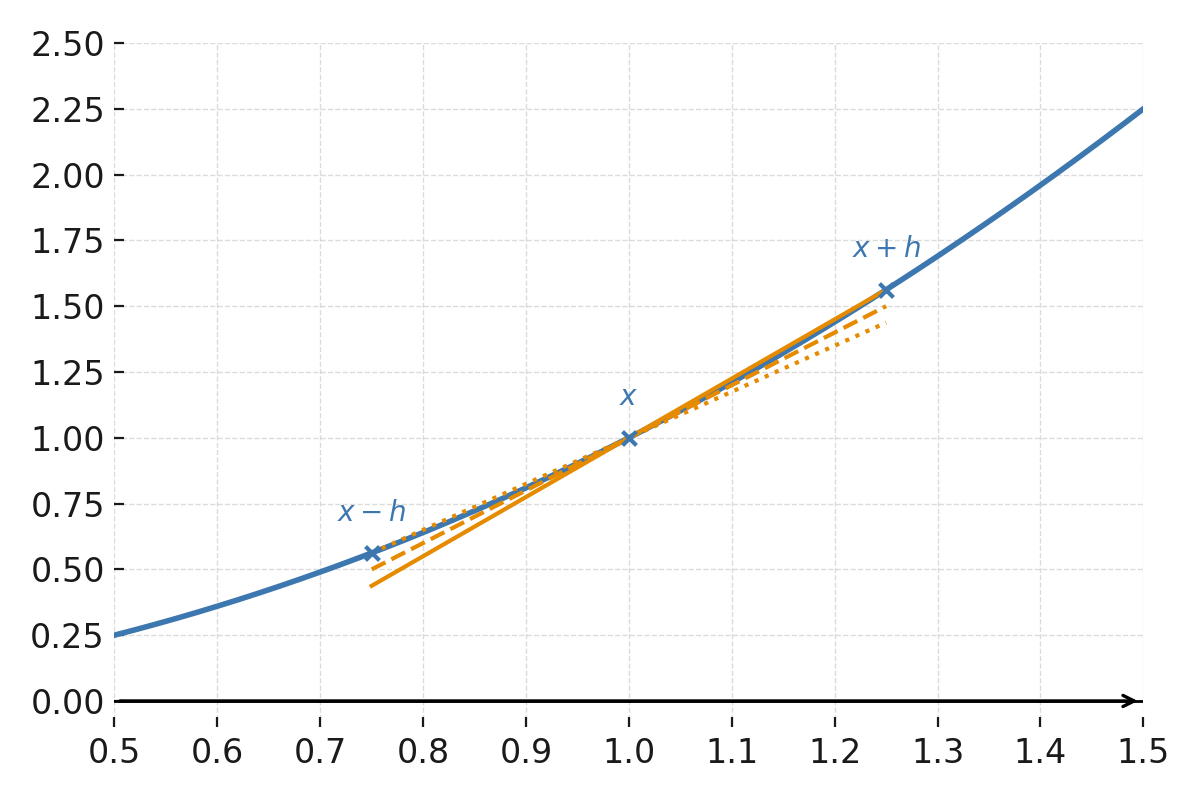
Die Funktion \( \large f(x) = x^2 \) um den Punkt \( \large x=1 \).
Die drei Steigungen (vorwärts, rückwärts und zentral) zeigen den Unterschied zwischen der Verwendung der Punkte \( \large (x,f(x)) \), \( \large (x+h,f(x+h)) \) und \( \large (x-h,f(x-h)) \).
Hinweise
Die Genauigkeit hängt davon ab, wie klein \( \large h \) gewählt wird. Ein zu großes \( \large h \) ergibt eine schlechte Näherung, während ein zu kleines \( \large h \) Rundungsfehler verursachen kann. In der Praxis wird \( \large h \) so gewählt, dass der Differenzenquotient stabil ist und eine vernünftige Genauigkeit bietet.