Numerische Differentialgleichungen (Euler, Runge-Kutta)

Wenn eine Differentialgleichung nicht analytisch gelöst werden kann, kann eine angenäherte Lösung mithilfe numerischer Methoden gefunden werden. Diese Methoden berechnen die Funktionswerte Schritt für Schritt aus der Differentialgleichung und einer Anfangsbedingung. Zwei der am häufigsten verwendeten Verfahren sind die Euler-Methode und die Runge–Kutta-Methode.

Idee der numerischen Differentialgleichungen

Eine einfache gewöhnliche Differentialgleichung hat die Form:

$$ \large y' = f(x,y) $$

Wenn ein Anfangswert $ \large y(x_0) = y_0 $ bekannt ist, kann $ \large f(x,y) $ verwendet werden, um zu berechnen, wie sich $ y $ ändert, wenn $ x $ geringfügig zunimmt. Dieser Vorgang wird schrittweise wiederholt, um nach und nach eine numerische Lösung zu erzeugen.

Euler-Methode

Die Euler-Methode ist die einfachste numerische Lösung. Sie verwendet die Differentialgleichung direkt, um den nächsten Wert zu berechnen:

$$ \large y_{n+1} = y_n + h \cdot f(x_n, y_n) $$

Hierbei ist $ \large h $ die Schrittweite. Durch Wiederholen vieler kleiner Schritte kann eine angenäherte Kurve von $ y(x) $ gezeichnet werden.

Beispiel für die Euler-Methode

Wir wollen $ \large y' = y $ mit der Anfangsbedingung $ \large y(0) = 1 $ und $ \large h = 0{,}5 $ lösen.

Für jeden Schritt gilt:

$$ \large y_{n+1} = y_n + 0{,}5 \cdot y_n = 1{,}5y_n $$

Nach vier Schritten erhält man:

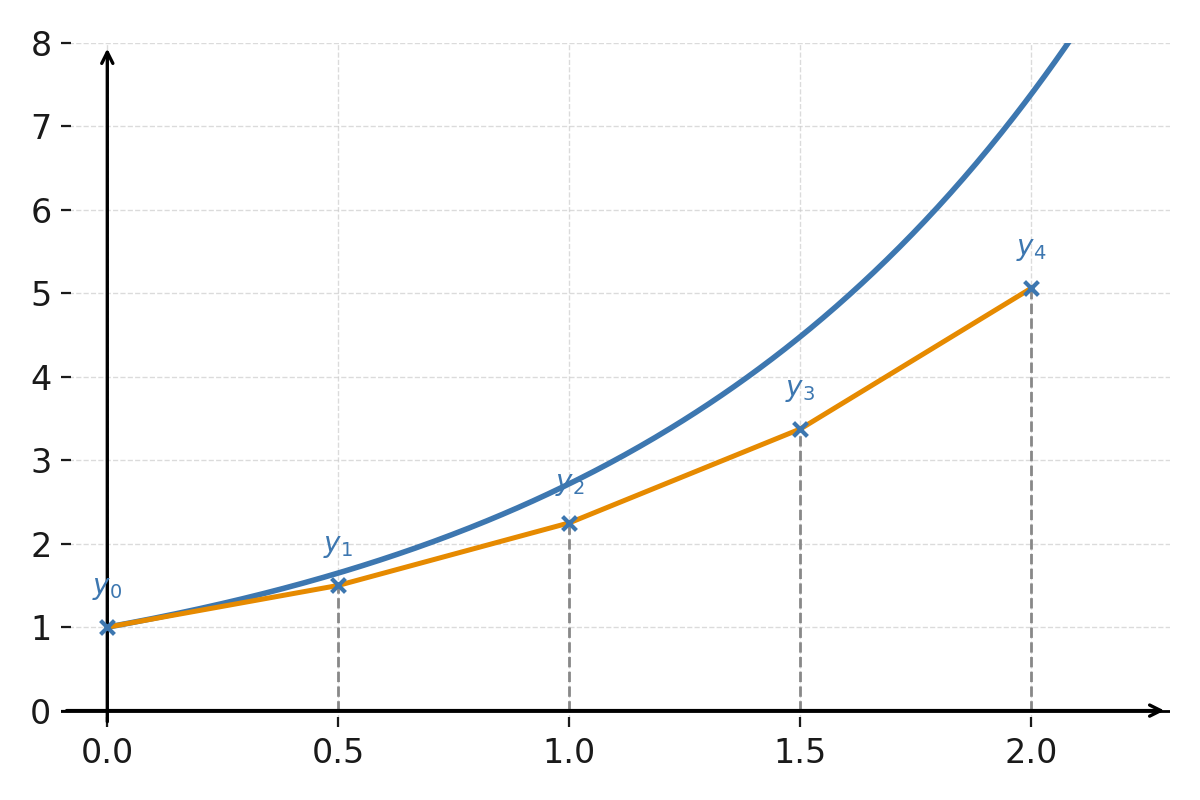
$$ \large y_1 = 1{,}5, \quad y_2 = 2{,}25, \quad y_3 = 3{,}375, \quad y_4 = 5{,}0625 $$

Die exakte Lösung lautet $ \large y = e^x $, und für $ \large x=2 $ ergibt sich $ \large e^2 \approx 7{,}389 $. Die Euler-Methode unterschätzt also die wahre Kurve, da jeder Schritt eine Gerade anstelle der gekrümmten Funktion verwendet.

Euler-Methode

Runge–Kutta-Methode (4. Ordnung)

Für eine bessere Genauigkeit kann die Runge–Kutta-Methode 4. Ordnung (RK4) verwendet werden. Sie bildet den Durchschnitt aus vier Steigungen statt nur einer:

$$
\large
\begin{aligned}
k_1 &= f(x_n, y_n) \\[8pt]
k_2 &= f\!\left(x_n + \frac{h}{2},\, y_n + \frac{h}{2}k_1\right) \\[8pt]
k_3 &= f\!\left(x_n + \frac{h}{2},\, y_n + \frac{h}{2}k_2\right) \\[8pt]
k_4 &= f\!\left(x_n + h,\, y_n + h k_3\right) \\[8pt]
y_{n+1} &= y_n + \frac{h}{6}\!\left(k_1 + 2k_2 + 2k_3 + k_4\right)
\end{aligned}
$$

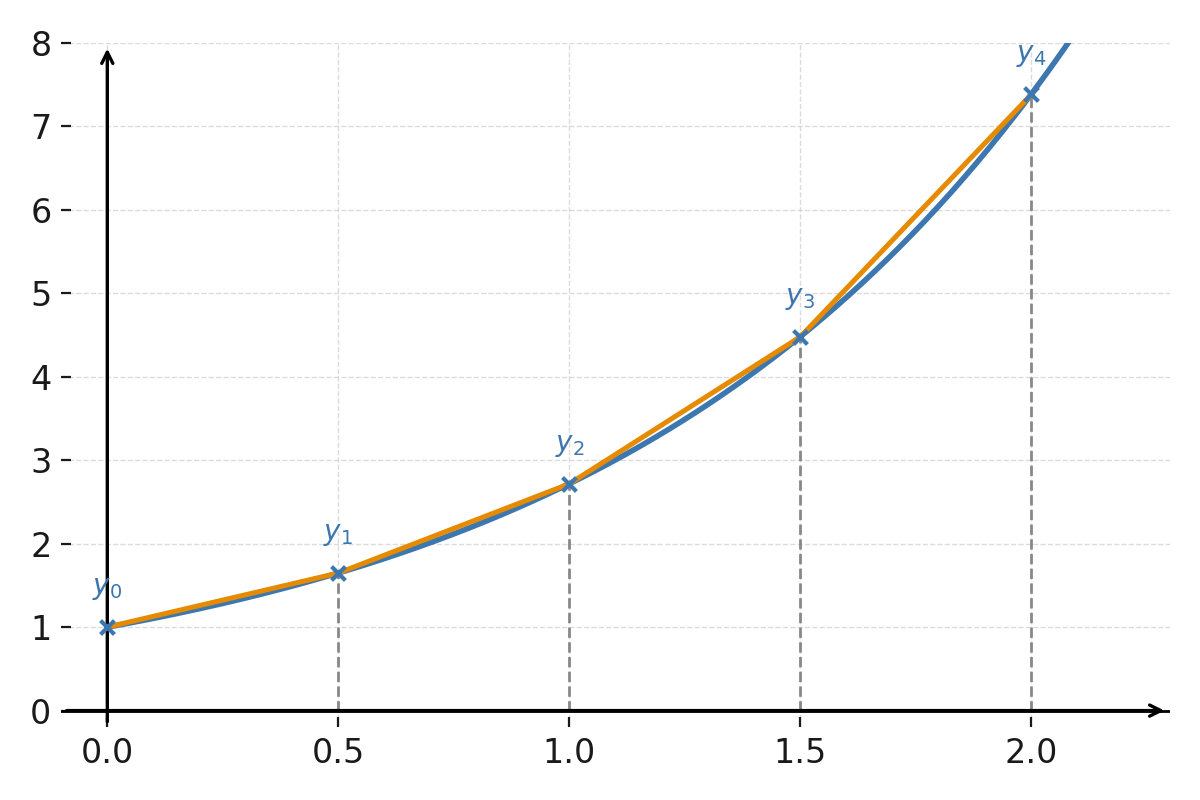
RK4 ist deutlich genauer als die Euler-Methode, selbst bei wenigen Schritten, und wird daher in der Praxis häufig verwendet.

Runge-Kutta-Methode

Hinweise

Numerische Differentialgleichungen gehören zu den wichtigsten Werkzeugen in der angewandten Mathematik, Physik und Technik. Sie werden verwendet, um Systeme zu simulieren, bei denen die Änderungsrate bekannt ist, jedoch keine geschlossene Formel für die Funktion existiert.