Sekantenmethode

Das Sekantenverfahren ist eine numerische Methode, um eine Nullstelle einer Funktion zu finden, also einen Punkt, an dem $ \large f(x) = 0 $ gilt. Es ähnelt dem Newton-Raphson-Verfahren, aber anstatt die Ableitung $ \large f'(x) $ zu verwenden, wird die Tangente durch eine Sekante ersetzt, die durch zwei Punkte der Kurve verläuft.

Idee der Methode

In jedem Schritt werden die beiden letzten Punkte $ \large (x_{n-1}, f(x_{n-1})) $ und $ \large (x_n, f(x_n)) $ verwendet, um eine Gerade (Sekante) zu bilden. Der Schnittpunkt dieser Sekante mit der x-Achse wird als neue Schätzung $ \large x_{n+1} $ verwendet. Die Methode wird wiederholt, bis zwei aufeinanderfolgende Schätzungen sehr nahe beieinander liegen.

Formel

$$ \large x_{n+1} = x_n - f(x_n) \cdot \frac{x_n - x_{n-1}}{f(x_n) - f(x_{n-1})} $$

Schrittweises Vorgehen

Wähle zwei Startwerte $ \large x_0 $ und $ \large x_1 $, bei denen die Funktion unterschiedliche Vorzeichen hat.
Berechne $ \large f(x_0) $ und $ \large f(x_1) $.
Verwende die Formel, um $ \large x_2 $ zu berechnen.
Wiederhole die Berechnung, sodass $ \large x_{n+1} $ aus den beiden letzten Punkten $ \large x_n $ und $ \large x_{n-1} $ berechnet wird.
Beende die Berechnung, wenn $ \large |x_{n+1} - x_n| < \varepsilon $.

Beispiel

Wir suchen die Nullstelle von $ \large f(x) = x^3 - x - 2 $.

Wähle $ \large x_0 = 1 $ und $ \large x_1 = 2 $.

$$ \large f(1) = -2, \quad f(2) = 4 $$

$$ \large x_2 = 2 - 4 \cdot \frac{2 - 1}{4 - (-2)} $$

$$ \large x_2 = 2 - 4 \cdot \frac{1}{6} $$

$$ \large x_2 = 1{,}333 $$

Der neue Punkt $ \large x_2 = 1{,}333 $ wird zusammen mit $ \large x_1 = 2 $ verwendet, um den nächsten Wert zu berechnen:

$$ \large x_3 = 1{,}333 - f(1{,}333) \cdot \frac{1{,}333 - 2}{f(1{,}333) - f(2)} $$

Nach einigen Iterationen ergibt sich eine Nullstelle $ \large x \approx 1{,}521 $, dasselbe Ergebnis wie mit dem Newton-Raphson-Verfahren, jedoch ohne die Ableitung der Funktion zu kennen.

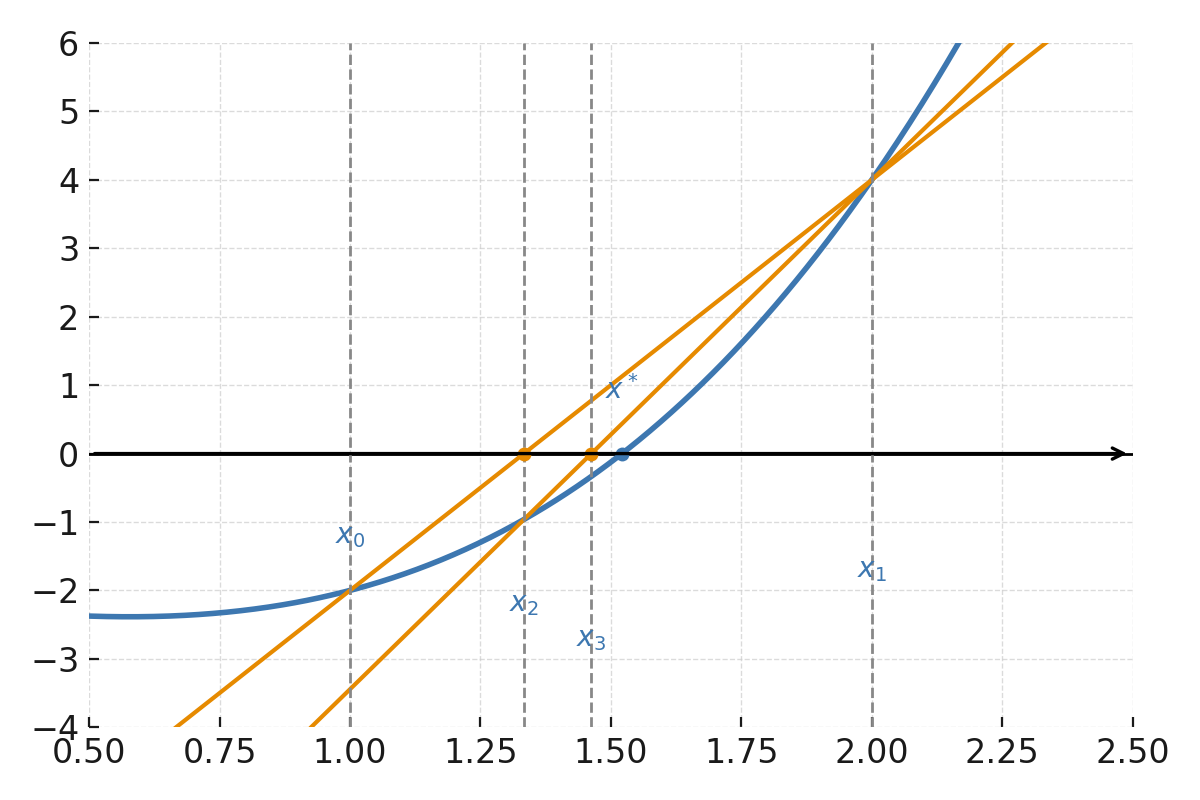
Sekantenverfahren - numerische Methoden

Die Funktion $ \large f(x) = x^3 - x - 2 $.

Die Punkte $ \large (x_0, f(x_0)) $ und $ \large (x_1, f(x_1)) $ werden durch eine Sekante verbunden, die die x-Achse bei $ \large x_2 $ schneidet. Danach wird eine neue Sekante zwischen $ \large (x_1, f(x_1)) $ und $ \large (x_2, f(x_2)) $ gezogen, die die Achse noch näher an der Nullstelle schneidet.

Hinweise

Das Sekantenverfahren konvergiert schneller als das Bisektionsverfahren, jedoch langsamer als Newton-Raphson. Es ist jedoch oft ein guter Kompromiss, da keine Ableitung der Funktion berechnet werden muss.