Newton-Raphson Methode

Das Newton-Raphson-Verfahren ist eine schnelle numerische Methode zum Finden von Nullstellen einer Funktion, also von Punkten, an denen $ \large f(x) = 0 $ gilt. Die Methode verwendet sowohl den Funktionswert als auch die Ableitung der Funktion, um die Schätzung der Position der Nullstelle zu verbessern.

Idee der Methode

Ausgangspunkt ist eine Anfangsschätzung $ \large x_0 $. Im Punkt $ \large (x_0, f(x_0)) $ wird die Tangente an die Kurve gezeichnet. Der Schnittpunkt dieser Tangente mit der x-Achse wird als neue Schätzung $ \large x_1 $ verwendet. Der Prozess wird wiederholt, bis der Unterschied zwischen zwei aufeinanderfolgenden Schätzungen kleiner als eine gewählte Toleranz $ \large \varepsilon $ ist.

Formel

$$ \large x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)} $$

Schrittweises Vorgehen

Wähle einen Startwert $ \large x_0 $.
Berechne $ \large f(x_0) $ und $ \large f'(x_0) $.
Verwende die Formel, um $ \large x_1 $ zu berechnen.
Wiederhole, bis $ \large |x_{n+1} - x_n| < \varepsilon $.

Beispiel

Wir wollen die Nullstelle von $ \large f(x) = x^3 - x - 2 $ finden, die wir zuvor mit dem Bisektionsverfahren gelöst haben.

Die Ableitung ist $ \large f'(x) = 3x^2 - 1 $.

Wir wählen eine Anfangsschätzung $ \large x_0 = 1{,}5 $.

$$ \large f(1{,}5) = (1{,}5)^3 - 1{,}5 - 2$$

$$ \large f(1{,}5) = -0{,}125 $$

$$ \large f'(1{,}5) = 3(1{,}5)^2 - 1 $$

$$ \large f'(1{,}5) = 5{,}75 $$

$$ \large x_1 = 1{,}5 - \frac{-0{,}125}{5{,}75} $$

$$ \large x_1 = 1{,}5217 $$

Nach wenigen Iterationen konvergiert das Verfahren schnell gegen die Nullstelle $ \large x \approx 1{,}521 $.

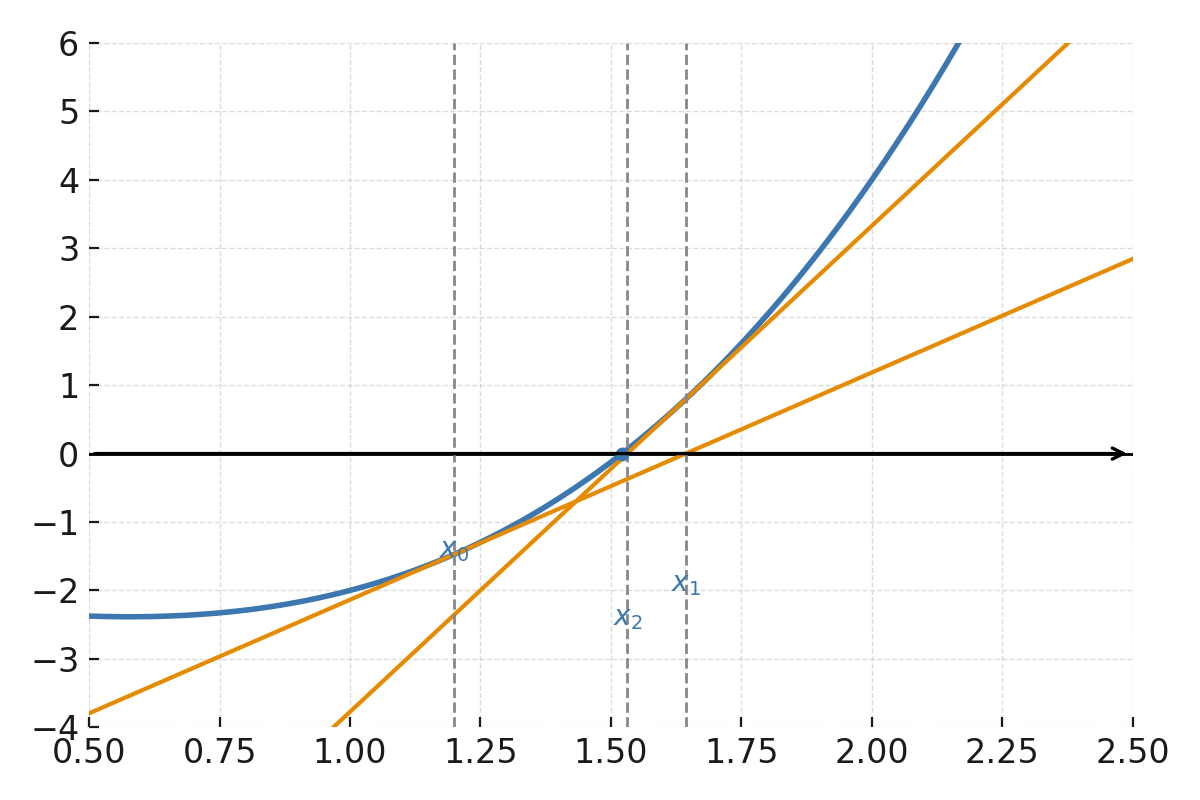
Newton-Raphson-Verfahren

Die Funktion $ \large f(x) = x^3 - x - 2 $. Die Anfangsschätzung $ \large x_0 $ ist auf der x-Achse markiert, und die Tangente in $ \large x_0 $ wird als Linie gezeigt, die die x-Achse bei $ \large x_1 $ schneidet. Danach wird die Tangente in $ \large x_1 $ gezeichnet, die die x-Achse noch näher an der Nullstelle schneidet. Die Abbildung zeigt die iterative Annäherung.

Hinweise

Das Newton-Raphson-Verfahren konvergiert deutlich schneller als das Bisektionsverfahren, erfordert jedoch, dass die Ableitung $ \large f'(x) $ berechnet werden kann und dass die Anfangsschätzung in der Nähe der tatsächlichen Nullstelle liegt. Wenn die Tangente fast waagerecht ist (d.h. $ \large f'(x) \approx 0 $), kann das Verfahren versagen oder die Nullstelle überspringen.