Skalarprodukt
Skalarproduktet er en operation mellem to vektorer, som giver et tal. Det bruges til at beregne vinkler mellem vektorer og til at afgøre, om de står vinkelret på hinanden.
Definition
For to vektorer i rummet \( \large \mathbf{u} = (x_1,y_1,z_1) \) og \( \large \mathbf{v} = (x_2,y_2,z_2) \) er skalarproduktet defineret som
$$ \large \mathbf{u} \cdot \mathbf{v} = x_1x_2 + y_1y_2 + z_1z_2 $$
En anden formel viser sammenhængen med vinklen mellem vektorerne:
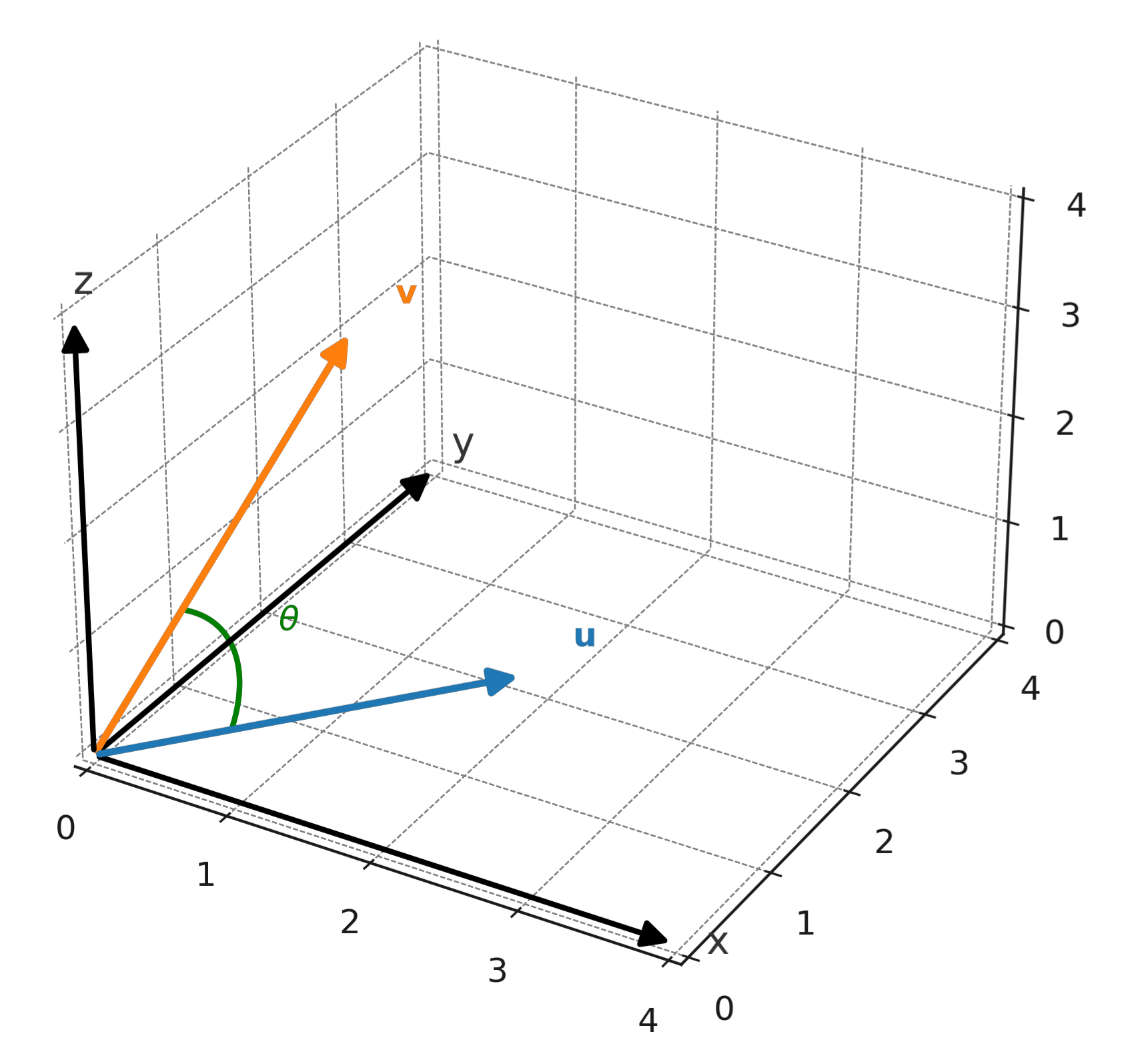
$$ \large \mathbf{u} \cdot \mathbf{v} = |\mathbf{u}| \cdot |\mathbf{v}| \cdot \cos(\theta) $$
hvor \( \large \theta \) er vinklen mellem \( \large \mathbf{u} \) og \( \large \mathbf{v} \).
Eksempel
Vi tager \( \large \mathbf{u} = (1,2,3) \) og \( \large \mathbf{v} = (4,-1,2) \).
$$ \large \mathbf{u} \cdot \mathbf{v} = 1 \cdot 4 + 2 \cdot (-1) + 3 \cdot 2 = 4 - 2 + 6 = 8 $$
Skalarproduktet er 8.
Geometrisk fortolkning
Skalarproduktet måler, hvor meget de to vektorer peger i samme retning. Er vinklen mindre end 90°, er skalarproduktet positivt. Er vinklen større end 90°, er skalarproduktet negativt. Er vektorerne vinkelrette, er skalarproduktet nul.
Anvendelse
Skalarproduktet bruges i mange sammenhænge, blandt andet til at finde vinkler mellem vektorer, til at afgøre ortogonalitet og i fysik til at beregne arbejde udført af en kraft langs en bevægelse.