Linjer og planer i rummet
I rummet kan linjer og planer beskrives ved hjælp af vektorer. Det gør det muligt at arbejde systematisk med geometri i tre dimensioner.
Linjer
En linje i rummet kan beskrives ved et punkt \( \large \mathbf{a} \) og en retningsvektor \( \large \mathbf{r} \). Alle punkter \( \large \mathbf{x} \) på linjen kan skrives som
$$ \large \mathbf{x} = \mathbf{a} + t \cdot \mathbf{r}, \quad t \in \mathbb{R} $$
Her angiver \( \large t \) en parameter, der bestemmer, hvor langt man bevæger sig langs linjen.
Eksempel
En linje gennem punktet \( \large (1,2,0) \) med retningsvektor \( \large (2,-1,3) \) er givet ved:
$$ \large \mathbf{x} = (1,2,0) + t \cdot (2,-1,3) $$
Planer
En plan kan beskrives ved et punkt \( \large \mathbf{a} \) og en normalvektor \( \large \mathbf{n} \). Alle punkter \( \large \mathbf{x} \) i planen opfylder
$$ \large (\mathbf{x} - \mathbf{a}) \cdot \mathbf{n} = 0 $$
Dette betyder, at forskellen mellem ethvert punkt i planen og punktet \( \large \mathbf{a} \) står vinkelret på normalvektoren.
Eksempel
En plan gennem punktet \( \large (1,0,2) \) med normalvektor \( \large (2,-1,1) \) kan beskrives som
$$ \large 2(x-1) -1(y-0) + 1(z-2) = 0 $$
eller omskrevet:
$$ \large 2x - y + z = 4 $$
Geometrisk fortolkning
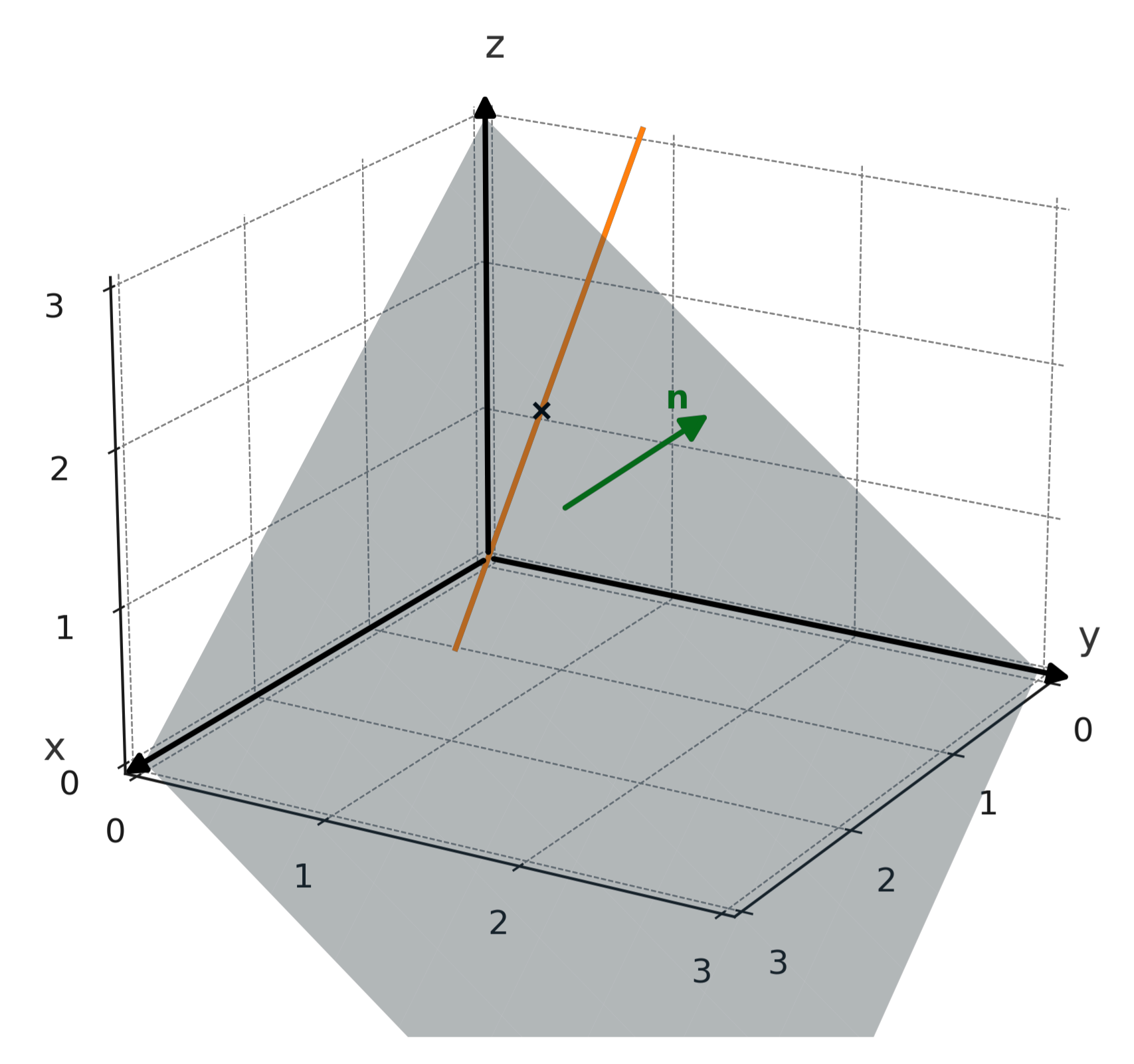
En linje beskriver alle punkter langs en retning, mens en plan beskriver alle punkter i et uendeligt "fladt lag". Normalvektoren (n) til en plan peger vinkelret på denne flade.
Skæringen mellem en linje og en plan kan være et enkelt punkt, som markeret med kryds på illustartionen herunder.
Det kan også være hele linjen, hvis linjen ligger i planen, eller det kan være tomt, hvis linjen er parallel med og uden for planen.
Anvendelse
Linjer og planer i rummet er centrale i geometri, fysik og datalogi. De bruges bl.a. til at beskrive bevægelsesbaner, spejlinger, 3D-modellering og kollisionsdetektering i computer-grafik.