Rumfang med vektorer

Rumfang af en figur i rummet kan beregnes ved hjælp af vektorer. Særligt parallelepipeder (kasser) kan udtrykkes på en enkel formel, når de beskrives af tre vektorer.

 

Rumfang af parallelepipedum

For tre vektorer \( \large \mathbf{u}, \mathbf{v}, \mathbf{w} \) i rummet gælder, at rumfanget af parallelepipedet udspændt af dem er givet ved:

 

$$ \large V = \left| \det \begin{pmatrix} x_1 & x_2 & x_3 \\ y_1 & y_2 & y_3 \\ z_1 & z_2 & z_3 \end{pmatrix} \right| $$

 

hvor \( \large \mathbf{u} = (x_1,y_1,z_1) \), \( \large \mathbf{v} = (x_2,y_2,z_2) \) og \( \large \mathbf{w} = (x_3,y_3,z_3) \).

 

 

Eksempel

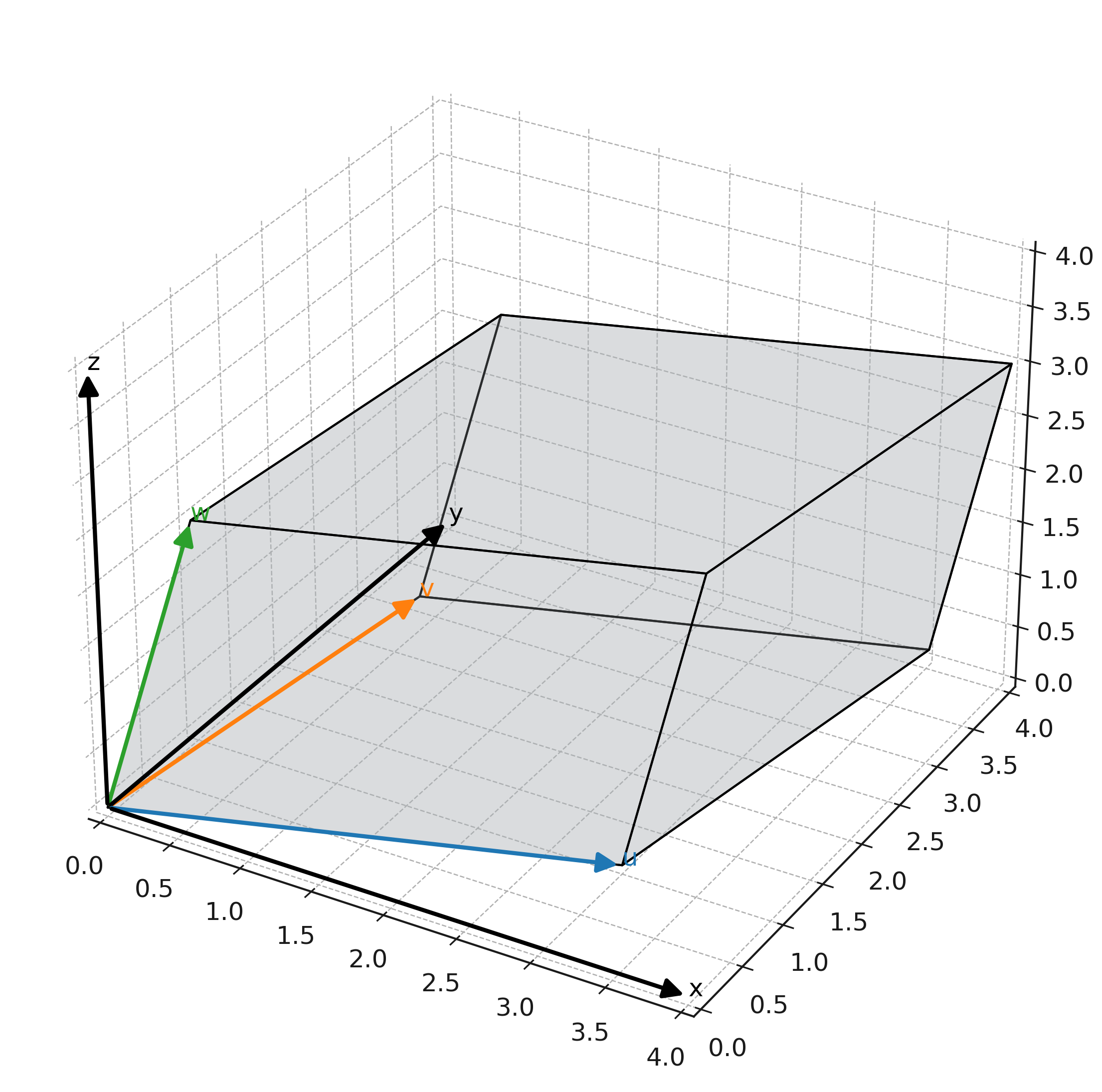
Vi tager \( \large \mathbf{u} = (3,1,0) \), \( \large \mathbf{v} = (1,2,1) \) og \( \large \mathbf{w} = (0,1,2) \).

 

$$ \large V = \left| \det \begin{pmatrix} 3 & 1 & 0 \\ 1 & 2 & 1 \\ 0 & 1 & 2 \end{pmatrix} \right| $$

 

Når man skal regne en determinant ud, kan man udvide den efter en vilkårlig række eller søjle. Resultatet bliver altid det samme, uanset hvilken man vælger. For nemheds skyld udvider vi her efter første række.

 

$$ \large V= 3 \cdot \det \begin{pmatrix} 2 & 1 \\ 1 & 2 \end{pmatrix} - 1 \cdot \det \begin{pmatrix} 1 & 1 \\ 0 & 2 \end{pmatrix} + 0 \cdot \det \begin{pmatrix} 1 & 2 \\ 0 & 1 \end{pmatrix} $$

 

De små determinanter regnes ud hver for sig:

$$ \large \det \begin{pmatrix} 2 & 1 \\ 1 & 2 \end{pmatrix} = 2 \cdot 2 - 1 \cdot 1 = 3 $$

$$ \large \det \begin{pmatrix} 1 & 1 \\ 0 & 2 \end{pmatrix} = 1 \cdot 2 - 1 \cdot 0 = 2 $$

 

Vi indsætter nu resultaterne tilbage i udtrykket:

 

$$ \large V = | 3 \cdot 3 - 1 \cdot 2 + 0 | = | 9 - 2 | = | 7 | = 7 $$

 

Rumfanget af parallelepipedet er derfor 7. Vi bruger den absolutte værdi, fordi en determinant kan blive negativ afhængigt af vektorernes orientering, men rumfang kan aldrig være mindre end nul.

 

 

Geometrisk fortolkning

Formlen svarer til, at man beregner grundflade gange højde. Grundfladen findes ved hjælp af et areal, og højden findes ved at projicere den tredje vektor vinkelret på grundfladen.

 

Anvendelse

Rumfangsformler med vektorer bruges i geometri, lineær algebra og fysik. De gør det muligt at beregne rumfang af kasser og andre figurer i koordinatsystemer, og danner grundlag for videre emner som determinanter, krydsprodukt og integraler.