Krydsprodukt

Krydsproduktet af to vektorer i rummet er en vektor, der står vinkelret på begge de oprindelige vektorer. Krydsproduktet bruges til at finde arealer, normalvektorer og orienteringer i 3D-geometrien.

Definition

For to vektorer $ \large \mathbf{u} = (x_1,y_1,z_1) $ og $ \large \mathbf{v} = (x_2,y_2,z_2) $ er krydsproduktet defineret ved determinanten:

$$ \large \mathbf{u} \times \mathbf{v} = \begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ x_1 & y_1 & z_1 \\ x_2 & y_2 & z_2 \end{vmatrix} = (y_1z_2 - z_1y_2,\; z_1x_2 - x_1z_2,\; x_1y_2 - y_1x_2) $$

Eksempel

Vi tager $ \large \mathbf{u} = (1,2,3) $ og $ \large \mathbf{v} = (4,5,6) $.

$$ \large \mathbf{u} \times \mathbf{v} = \begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ 1 & 2 & 3 \\ 4 & 5 & 6 \end{vmatrix} = (-3,6,-3) $$

Resultatet er en ny vektor $ \large (-3,6,-3) $, der står vinkelret på både $ \large \mathbf{u} $ og $ \large \mathbf{v} $.

Geometrisk fortolkning

Længden af krydsproduktet svarer til arealet af parallelogrammet, som vektorerne udspænder:

$$ \large |\mathbf{u} \times \mathbf{v}| = |\mathbf{u}| \cdot |\mathbf{v}| \cdot \sin(\theta) $$

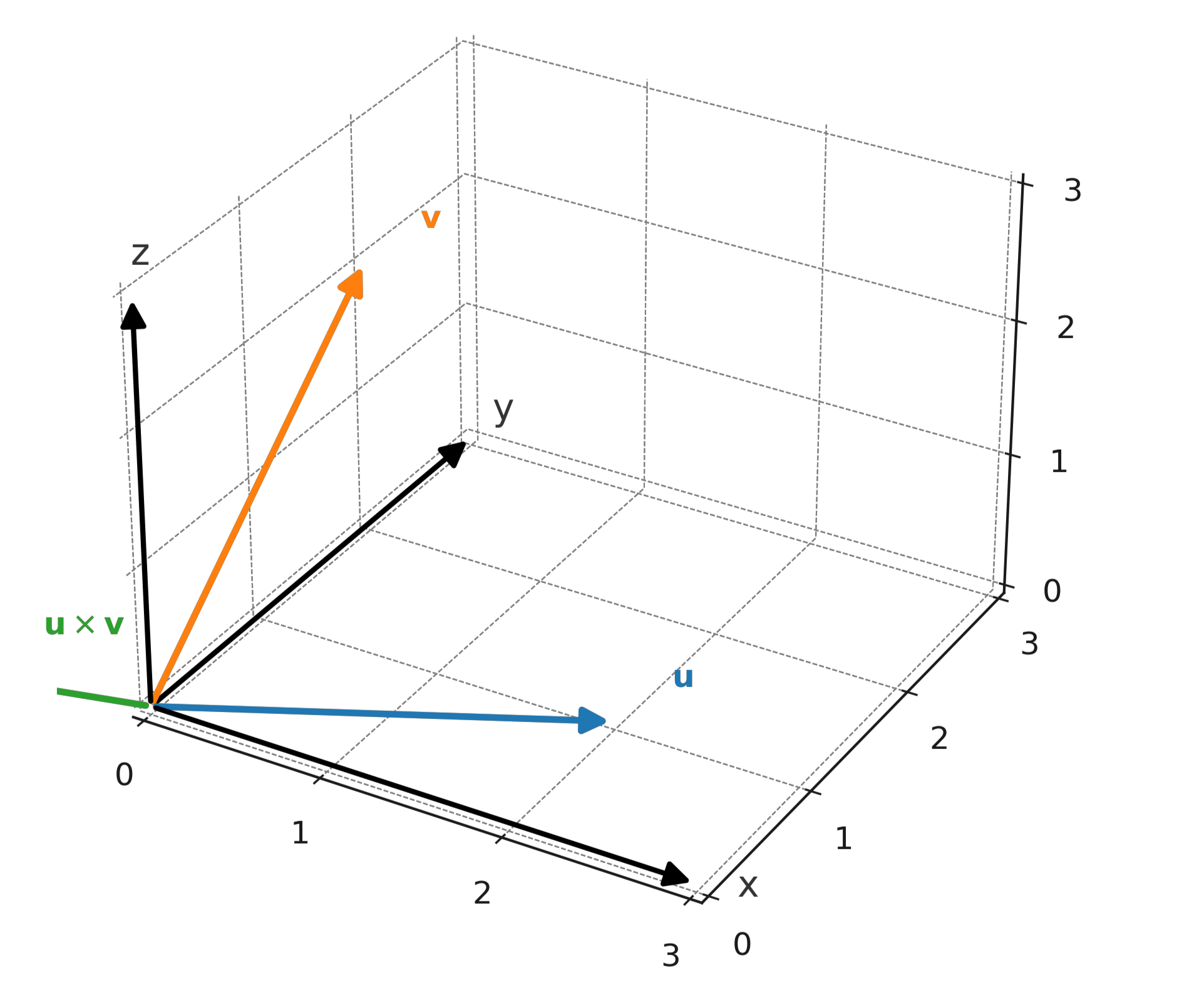
Retningen bestemmes af højrehåndsreglen: Hvis man peger højre hånds pegefinger i retning af $ \large \mathbf{u} $ og langfingeren i retning af $ \large \mathbf{v} $, vil tommelfingeren pege i retning af $ \large \mathbf{u} \times \mathbf{v} $.

Anvendelse

Krydsproduktet bruges mange steder i matematik og fysik:

Til at finde en normalvektor til et plan
Til at beregne arealet af parallelogrammer og trekanter i 3D
I mekanik til at bestemme moment af en kraft
I computer-grafik til at beregne fladers orientering