Koordinater i 3D
I 3D-rummet beskrives et punkt ved tre koordinater. Hvor vi i planen bruger to tal til at angive en position, kræves der i rummet tre tal for at bestemme et punkt entydigt.
Definition
Et punkt \( \large P \) i rummet angives som
$$ \large P = (x,y,z) $$
Her er \( \large x \) afstanden langs x-aksen, \( \large y \) afstanden langs y-aksen og \( \large z \) afstanden langs z-aksen.
Eksempel
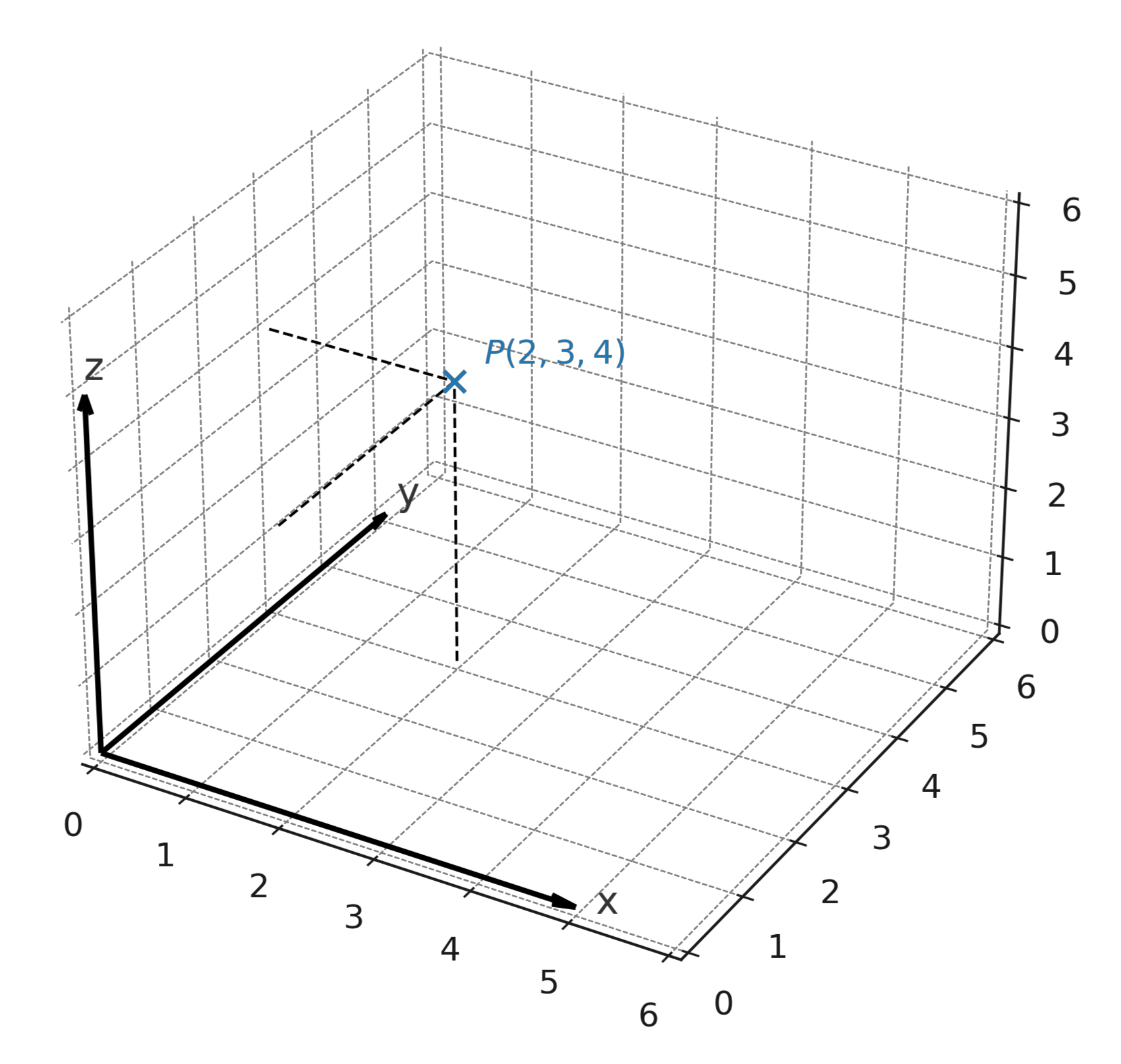
Punktet \( \large P = (2,3,4) \) betyder, at man går 2 enheder ud ad x-aksen, 3 enheder ud ad y-aksen og 4 enheder op ad z-aksen.
Koordinataksen og origo
De tre akser kaldes x-, y- og z-aksen. Deres fælles udgangspunkt kaldes origo og har koordinaterne
$$ \large O = (0,0,0) $$
En vektor fra origo til et punkt \( \large P=(x,y,z) \) skrives som
$$ \large \vec{OP} = (x,y,z) $$
Afstand i rummet
Afstanden fra origo til et punkt \( \large (x,y,z) \) findes ved at udvide Pythagoras’ sætning:
$$ \large |(x,y,z)| = \sqrt{x^2 + y^2 + z^2} $$
Dette er længden af vektoren fra origo til punktet.
Geometrisk fortolkning
Et koordinatsystem i rummet er bygget af tre indbyrdes vinkelrette akser. Hvert punkt kan ses som et hjørne i et rektangulært prisme med origo som udgangspunkt.
Anvendelse
Koordinater i 3D bruges overalt i matematik, fysik og datalogi, fx til at beskrive punkter i geometri, positioner i rummet eller objekter i 3D-grafik.