Projections

La projection d’un vecteur sur un autre décrit combien d’un vecteur pointe dans la direction de l’autre. Cela correspond à voir le vecteur comme une ombre projetée sur l’autre vecteur.

 

Définition

La projection de \( \large \mathbf{u} \) sur \( \large \mathbf{v} \) est donnée par :

 

$$ \large \text{proj}_{\mathbf{v}}(\mathbf{u}) = \frac{\mathbf{u} \cdot \mathbf{v}}{|\mathbf{v}|^2} \cdot \mathbf{v} $$

 

Exemple

Nous prenons \( \large \mathbf{u} = (3,4) \) et \( \large \mathbf{v} = (4,0) \).

 

On calcule d’abord le produit scalaire :

 

$$ \large \mathbf{u} \cdot \mathbf{v} = 3 \cdot 4 + 4 \cdot 0 = 12 $$

 

La longueur de \( \large \mathbf{v} \) est :

 

$$ \large |\mathbf{v}|^2 = 4^2 + 0^2 = 16 $$

 

La projection est donc :

 

$$ \large \text{proj}_{\mathbf{v}}(\mathbf{u}) = \frac{12}{16} \cdot (4,0) = (3,0) $$

 

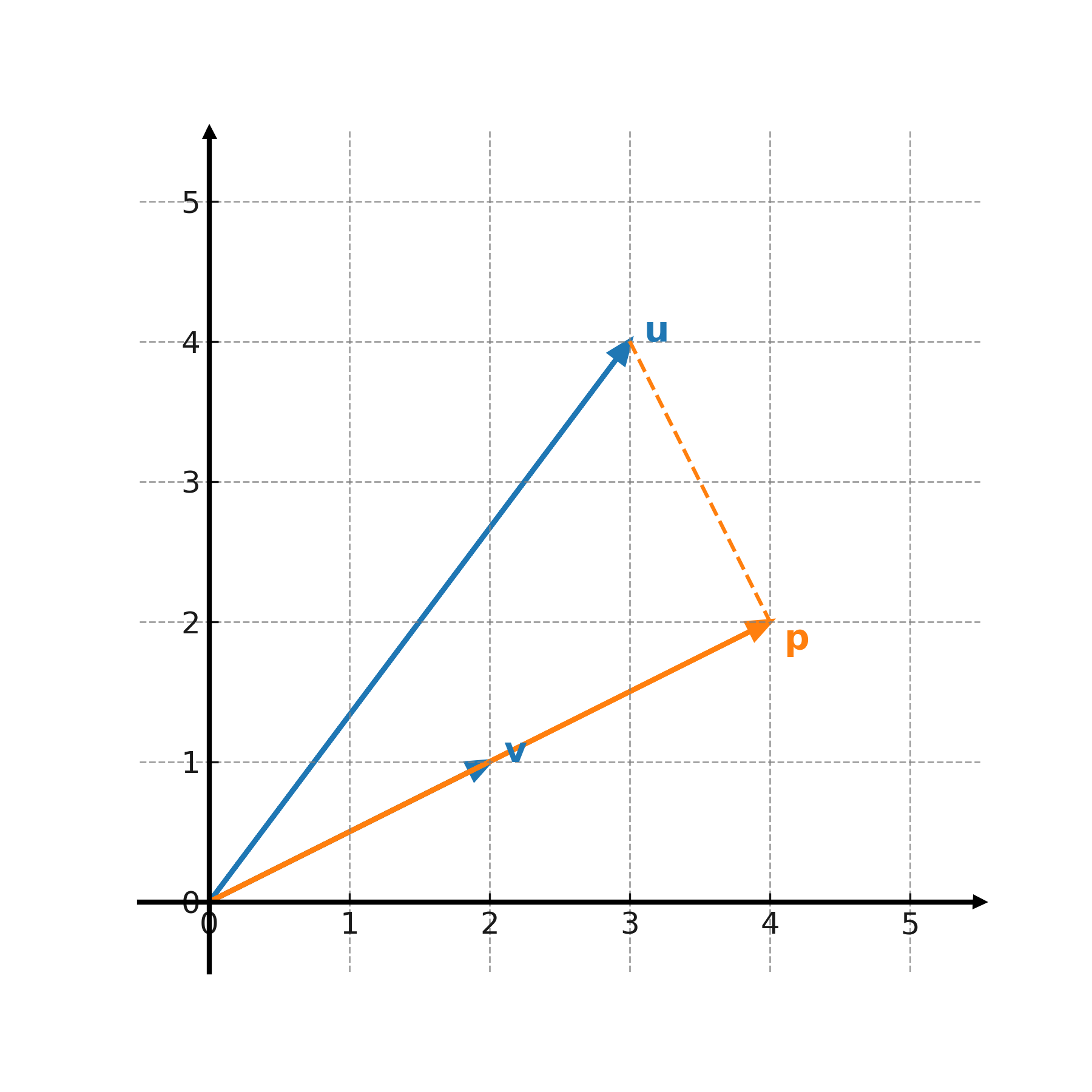
Interprétation géométrique

La projection est le vecteur qui se trouve sur \( \large \mathbf{v} \) et qui représente la partie de \( \large \mathbf{u} \) pointant dans la même direction. On peut la voir comme l’ombre de \( \large \mathbf{u} \) projetée sur la droite passant par \( \large \mathbf{v} \).

 

Remarque : La différence \( \large \mathbf{u} - \text{proj}_{\mathbf{v}}(\mathbf{u}) \) est toujours perpendiculaire à \( \large \mathbf{v} \). Ainsi, un vecteur peut être décomposé en une partie le long de \( \mathbf{v} \) et une partie perpendiculaire à \( \mathbf{v} \).

 

Si l’angle entre \( \mathbf{u} \) et \( \mathbf{v} \) est supérieur à \( 90^\circ \), la projection est dirigée vers l’arrière le long de \( \mathbf{v} \), ce qui donne une valeur scalaire négative devant \( \mathbf{v} \).

 

 

Application

Les projections sont souvent utilisées en physique pour calculer la composante d’une force agissant dans une direction spécifique, et en mathématiques pour trouver les composantes de vecteurs le long d’axes donnés.