Multiplication par un scalaire

Lorsqu’on multiplie un vecteur par un nombre, sa longueur change, mais la direction est conservée si le nombre est positif. Si le nombre est négatif, le vecteur est inversé dans la direction opposée.

 

Définition

Pour un vecteur \( \large \mathbf{v} = (x,y) \) et un nombre \( \large k \), on a :

 

$$ \large k \cdot (x,y) = (k \cdot x,\; k \cdot y) $$

 

Exemples

Considérons le vecteur \( \large \mathbf{v} = (2,1) \).

 

Quand \( \large k = 2 \) :

$$ \large 2 \cdot (2,1) = (4,2) $$

 

Quand \( \large k = -1 \) :

$$ \large -1 \cdot (2,1) = (-2,-1) $$

 

Quand \( \large k = \frac{1}{2} \) :

$$ \large \frac{1}{2} \cdot (2,1) = (1,\; \frac{1}{2}) $$

 

Quand \( \large k = 0 \) :

$$ \large 0 \cdot (2,1) = (0,0) $$

 

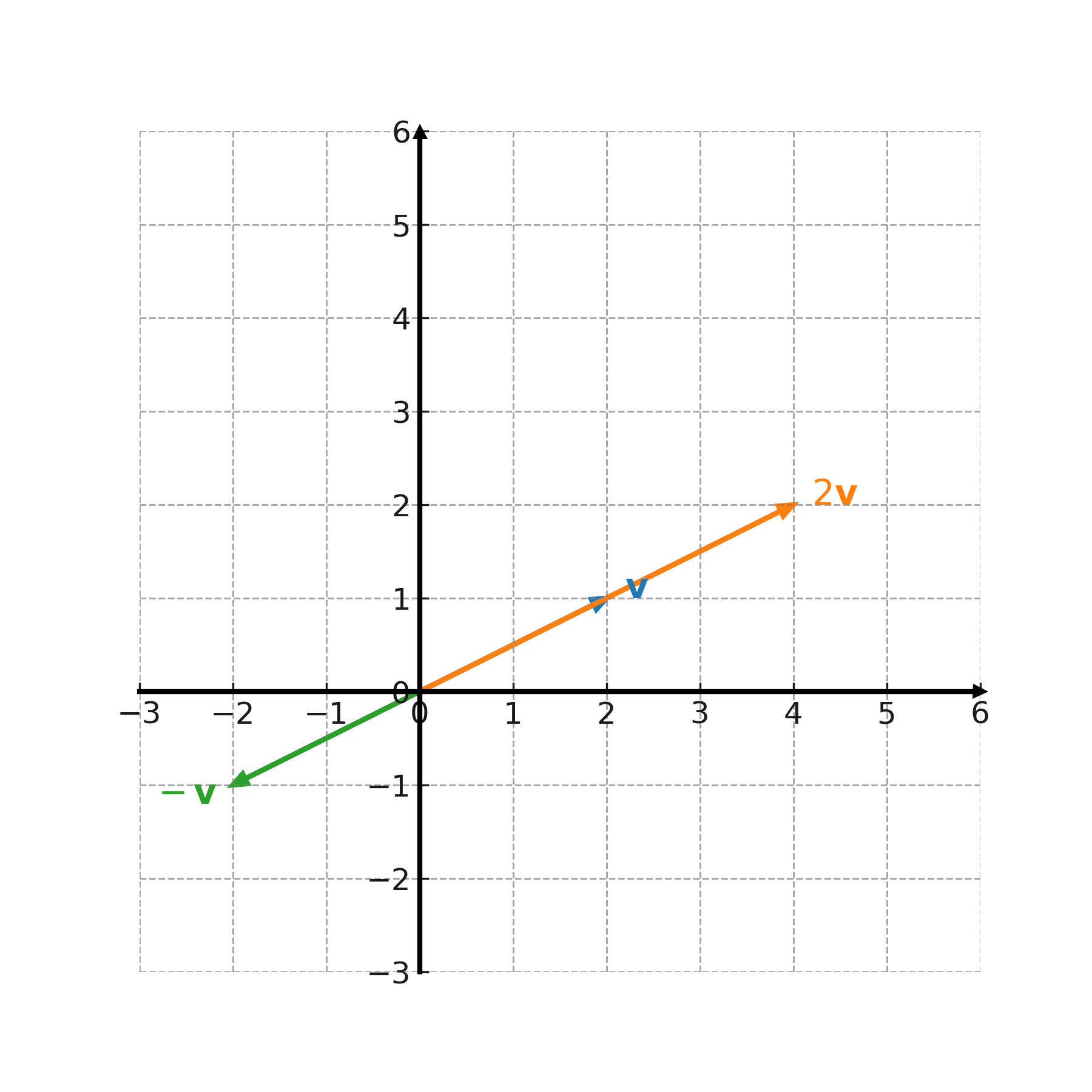
Interprétation géométrique

La multiplication par un nombre étire ou réduit le vecteur. Pour des nombres positifs, la direction est conservée; pour des nombres négatifs, la direction est inversée. Quand le nombre est compris entre 0 et 1, le vecteur devient plus court, et quand le nombre est 0, on obtient le vecteur nul.

 

 

Application

La multiplication par des nombres est utilisée pour modifier la grandeur d’un mouvement ou d’une force. En physique, cela correspond à modifier l’intensité d’une force sans en changer la direction.

 

En mathématiques, la multiplication par des paramètres est utilisée pour décrire des droites et des courbes, par exemple \( \large (x,y) = (x_0,y_0) + t \cdot \mathbf{r} \), où \( \large t \) est un nombre et \( \large \mathbf{r} \) un vecteur directeur.