Aire avec des vecteurs

L’aire d’une figure peut être calculée à l’aide de vecteurs. En particulier, les parallélogrammes et les triangles peuvent s’exprimer par une formule simple lorsqu’ils sont décrits par deux vecteurs.

 

 

Aire du parallélogramme et du triangle

Pour deux vecteurs \( \large \mathbf{u} \) et \( \large \mathbf{v} \) dans le plan, l’aire du parallélogramme qu’ils engendrent est :

 

$$ \large A = |\mathbf{u}| \cdot |\mathbf{v}| \cdot \sin(\theta) $$

 

où \( \large \theta \) est l’angle entre les vecteurs. La formule provient du calcul base fois hauteur, où la hauteur est trouvée comme la projection d’un vecteur sur une direction perpendiculaire à l’autre.

 

Une autre méthode consiste à utiliser le déterminant :

 

$$ \large A = \left| \det \begin{pmatrix} x_1 & x_2 \\ y_1 & y_2 \end{pmatrix} \right| $$

 

si \( \large \mathbf{u} = (x_1,y_1) \) et \( \large \mathbf{v} = (x_2,y_2) \).

 

 

Exemple

Nous prenons \( \large \mathbf{u} = (3,2) \) et \( \large \mathbf{v} = (1,4) \).

 

$$ \large A = \left| \det \begin{pmatrix} 3 & 1 \\ 2 & 4 \end{pmatrix} \right| = |3 \cdot 4 - 2 \cdot 1| = |10| = 10 $$

 

L’aire du parallélogramme est 10. 

L’aire du triangle défini par les mêmes deux vecteurs est la moitié, soit \( \large 5 \).

 

 

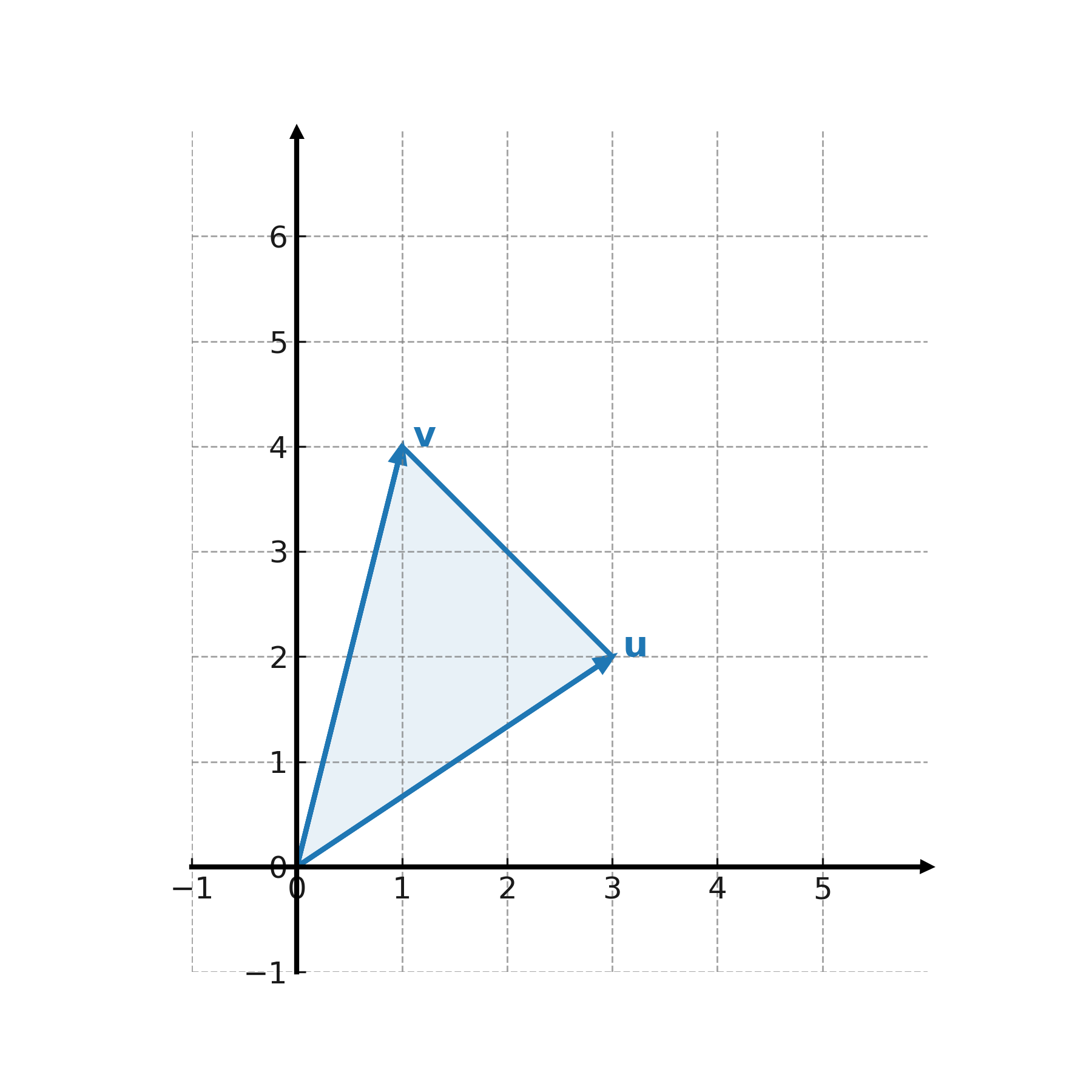
Interprétation géométrique

Le point essentiel à noter est que l’aire peut se calculer comme base fois hauteur, et que la hauteur peut être trouvée à l’aide de la projection. Ainsi, le concept de projection est étroitement lié au calcul d’aires.

 

 

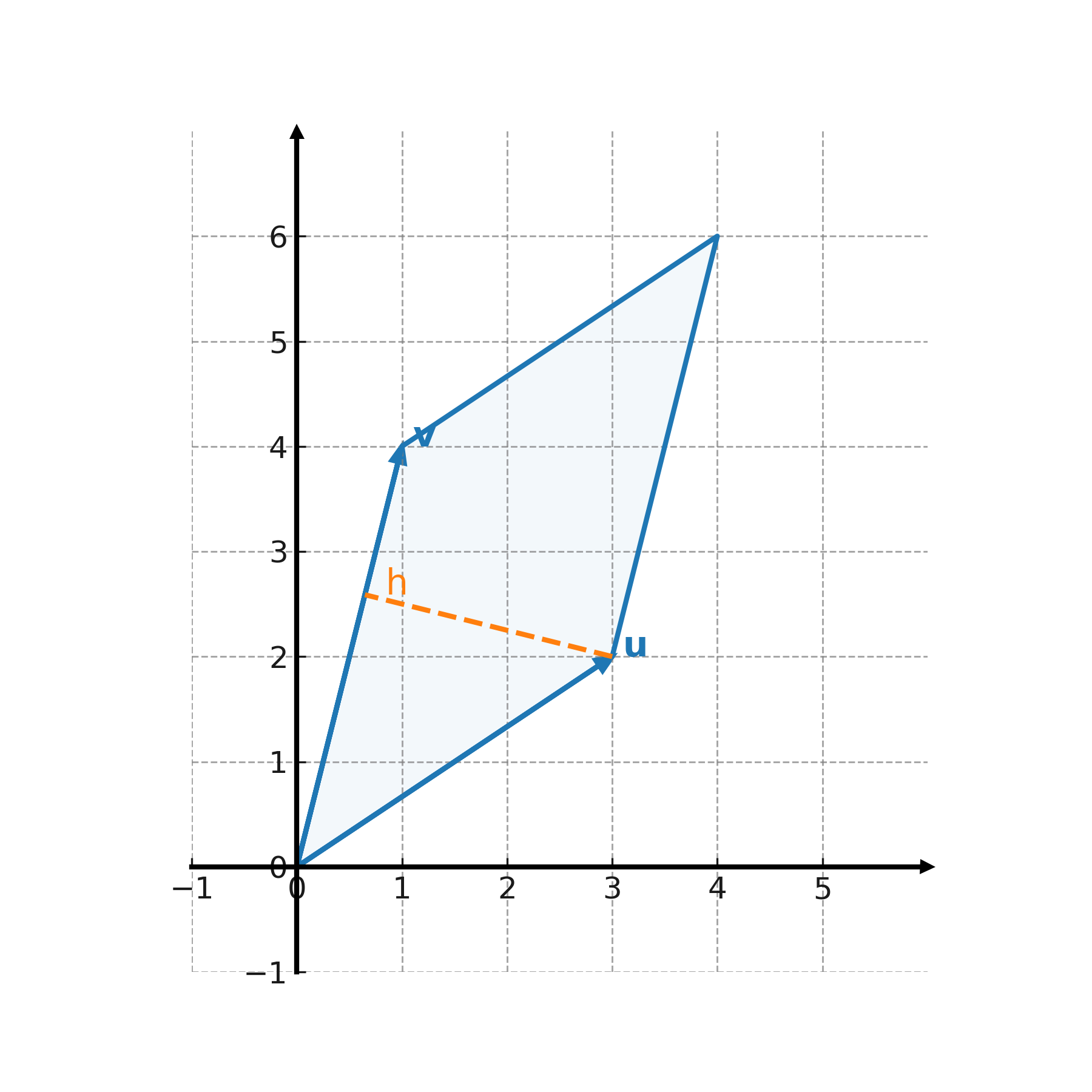
Application

Les formules vectorielles pour les aires sont utilisées en géométrie et en algèbre linéaire. Elles fournissent une méthode simple pour calculer des aires dans des systèmes de coordonnées et constituent la base de sujets ultérieurs tels que les déterminants et les volumes.