Longueur et vecteurs unitaires

La longueur d’un vecteur décrit la taille du vecteur, tandis qu’un vecteur unitaire est un vecteur de longueur 1 dans la même direction que l’original.

 

Longueur

Pour un vecteur \( \large \mathbf{v} = (x,y) \), la longueur se calcule ainsi :

 

$$ \large |\mathbf{v}| = \sqrt{x^2 + y^2} $$

 

Exemple : Le vecteur \( \large \mathbf{v} = (3,4) \) a pour longueur

 

$$ \large |\mathbf{v}| = \sqrt{3^2 + 4^2} = 5 $$

 

Vecteur unitaire

Un vecteur unitaire s’obtient en divisant un vecteur par sa longueur :

 

$$ \large \mathbf{e} = \frac{1}{|\mathbf{v}|} \cdot \mathbf{v} $$

 

Exemple : Pour \( \large \mathbf{v} = (3,4) \) on obtient

 

$$ \large \mathbf{e} = \frac{1}{5} \cdot (3,4) = \left(\frac{3}{5}, \frac{4}{5}\right) $$

 

Remarque : Le vecteur nul \( \large (0,0) \) ne peut pas être transformé en vecteur unitaire car sa longueur est 0 et on ne peut pas diviser par 0.

 

Les vecteurs unitaires les plus connus sont les vecteurs unitaires standards dans le système de coordonnées :

 

$$ \large \mathbf{i} = (1,0), \quad \mathbf{j} = (0,1) $$

 

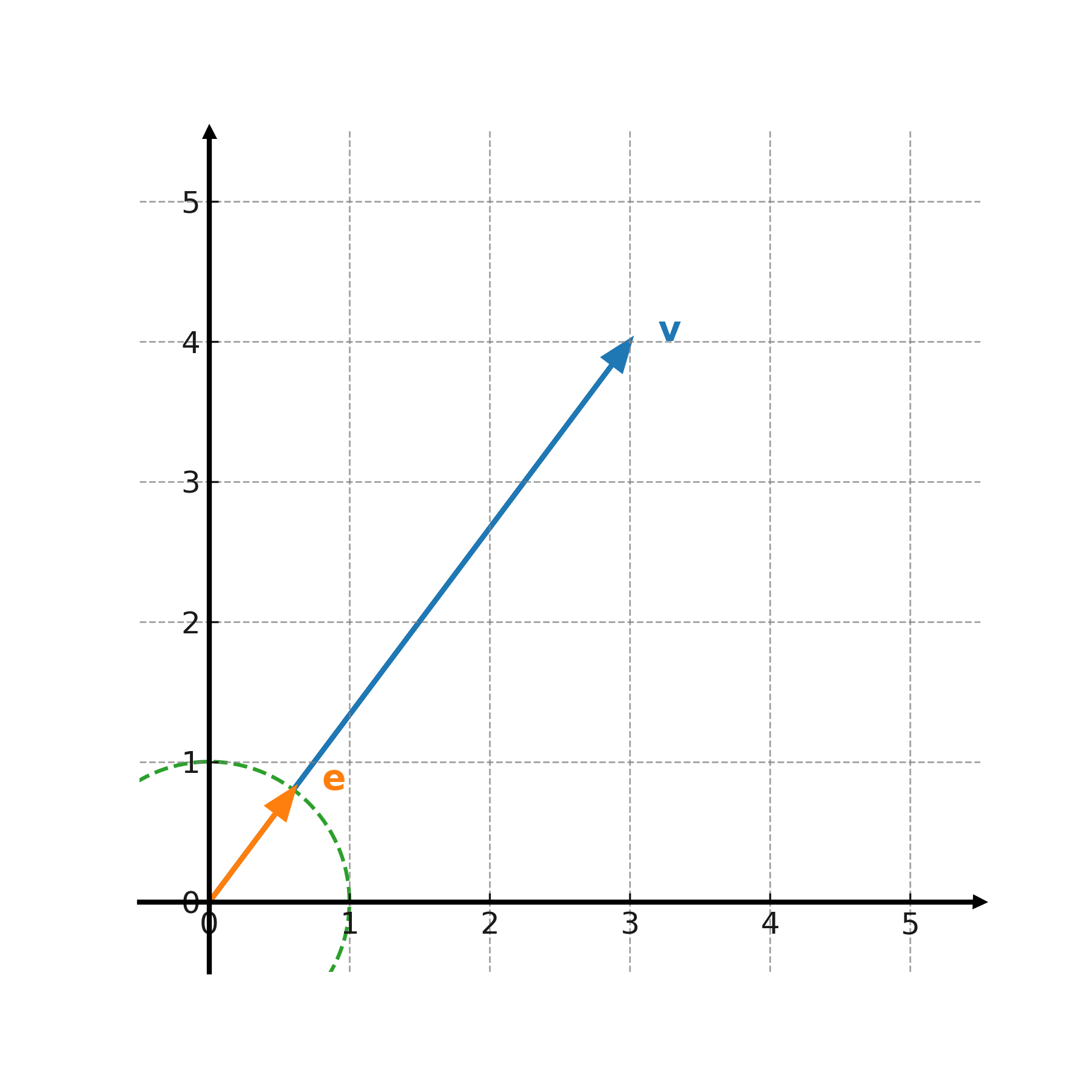
Interprétation géométrique

La longueur d’un vecteur correspond à la distance entre l’origine et l’extrémité du vecteur.

Un vecteur unitaire est une flèche dans la même direction, mais toujours de longueur 1.

 

 

Application

Les vecteurs unitaires sont utilisés pour décrire des directions, sans que la grandeur importe. En physique, ils servent par exemple à indiquer la direction d’une force indépendamment de son intensité, et en mathématiques ils sont utilisés pour définir les axes des systèmes de coordonnées.