Addition et soustraction

Lorsqu’on travaille avec des vecteurs dans le plan, on peut les additionner ou les soustraire. Cela se fait en combinant les coordonnées de chaque vecteur.

 

Définition

Pour deux vecteurs \( \large \mathbf{u} = (x_1,y_1) \) et \( \large \mathbf{v} = (x_2,y_2) \), on a :

 

$$ \large \mathbf{u} + \mathbf{v} = (x_1 + x_2,\; y_1 + y_2) $$

 

$$ \large \mathbf{u} - \mathbf{v} = (x_1 - x_2,\; y_1 - y_2) $$

 

 

Exemple

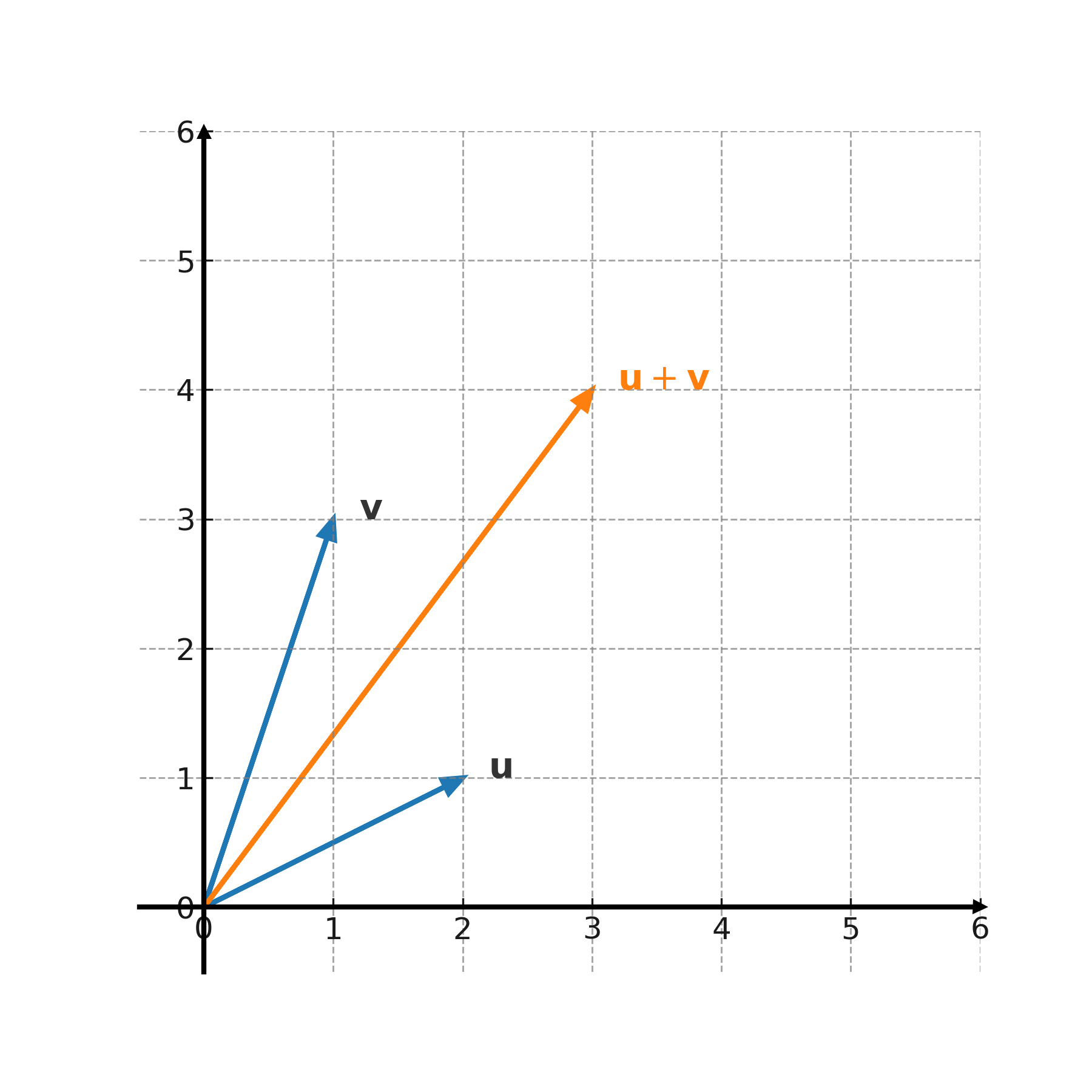
Nous voulons calculer la somme et la différence des vecteurs \( \large \mathbf{u} = (2,1) \) et \( \large \mathbf{v} = (1,3) \).

 

La somme est :

 

$$ \large (2,1) + (1,3) = (2+1,\; 1+3) = (3,4) $$

 

 

La différence est :

 

$$ \large (2,1) - (1,3) = (2-1,\; 1-3) = (1,-2) $$

 

 

Interprétation géométrique

L’addition peut être représentée graphiquement avec la méthode du parallélogramme : on place les vecteurs queue contre queue et on trace deux copies pour former un parallélogramme. La diagonale représente la somme.

 

 

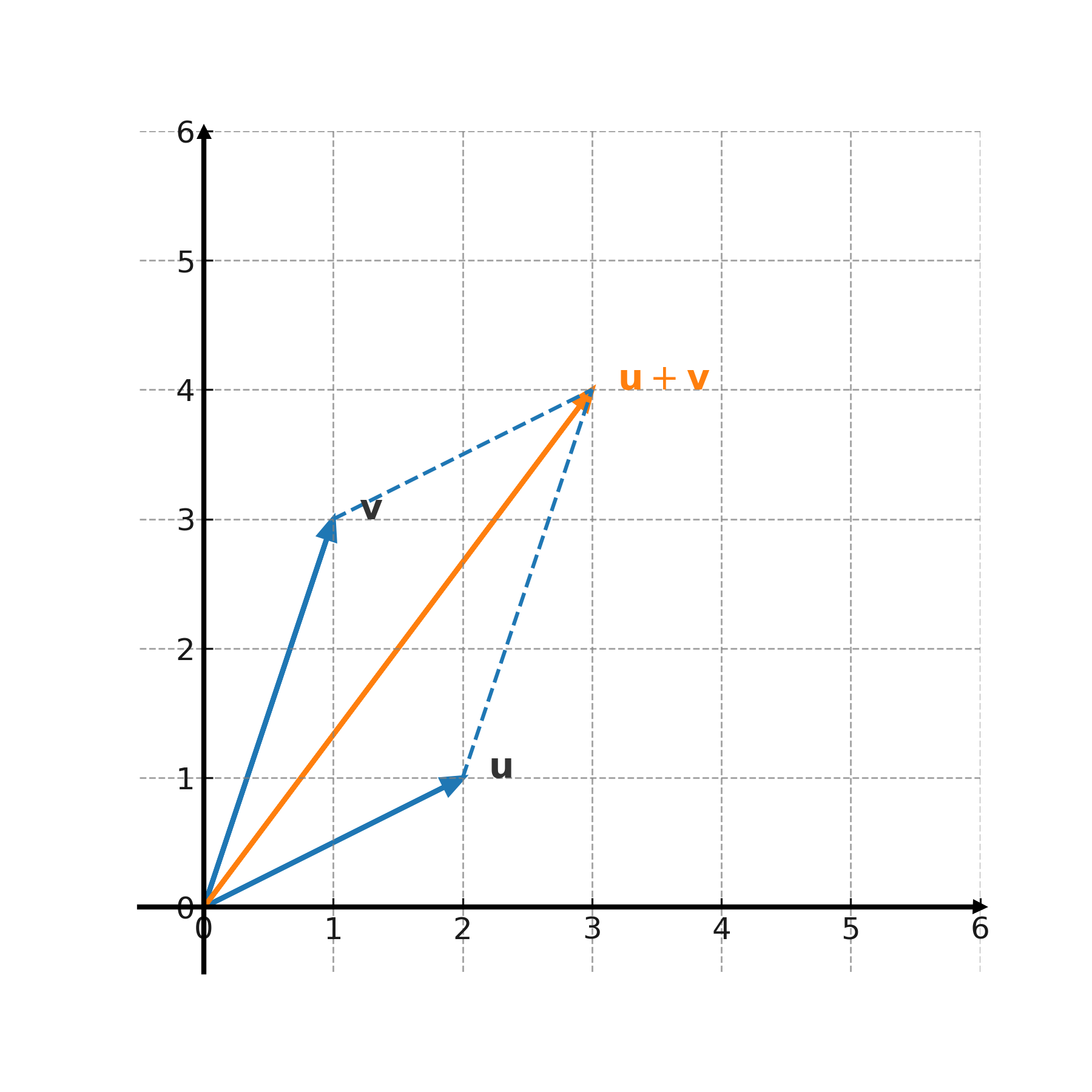
La soustraction peut être vue comme l’addition du vecteur opposé. Par exemple, \( \large \mathbf{u} - \mathbf{v} = \mathbf{u} + (-\mathbf{v}) \).

 

 

Application

En physique, l’addition de vecteurs est utilisée pour déterminer la force totale sur un corps. Si une boîte est tirée dans une direction par une force et dans une autre direction par une autre force, le mouvement résultant est donné par la somme des deux vecteurs de force.