Produit scalaire et angles

Le produit scalaire est une façon de combiner deux vecteurs qui donne un nombre. Il est utilisé, entre autres, pour déterminer l’angle entre deux vecteurs et pour savoir s’ils sont perpendiculaires.

 

Définition

Pour deux vecteurs \( \large \mathbf{u} = (x_1,y_1) \) et \( \large \mathbf{v} = (x_2,y_2) \), on a :

 

$$ \large \mathbf{u} \cdot \mathbf{v} = x_1 \cdot x_2 + y_1 \cdot y_2 $$

 

De plus, le produit scalaire peut s’écrire :

 

$$ \large \mathbf{u} \cdot \mathbf{v} = |\mathbf{u}| \cdot |\mathbf{v}| \cdot \cos(\theta) $$

 

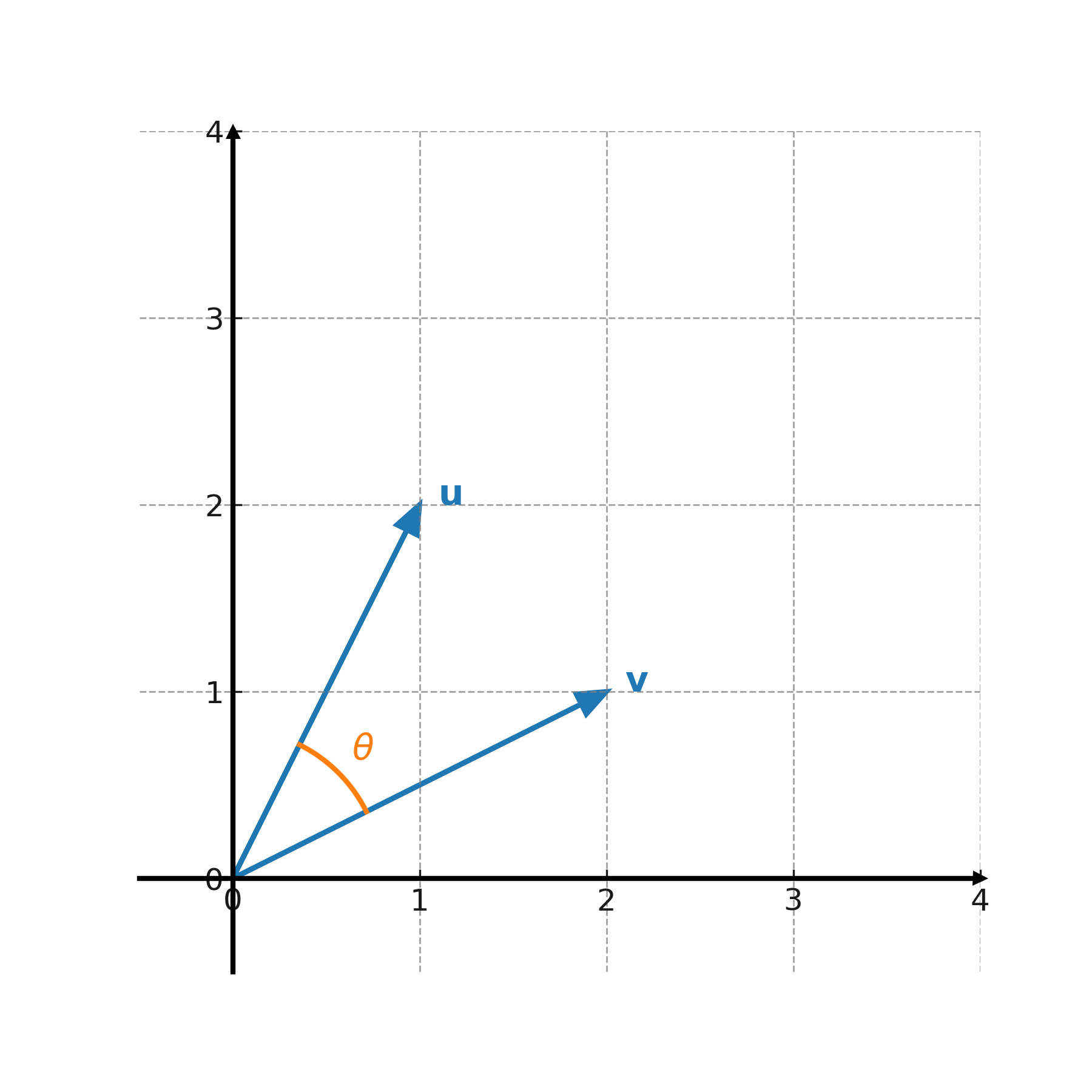
où \( \large \theta \) est l’angle entre les vecteurs.

 

 

Exemples

Exemple 1 :

 

$$ \large \mathbf{u} = (1,0), \; \mathbf{v} = (0,1) $$

$$ \large \mathbf{u} \cdot \mathbf{v} = 1 \cdot 0 + 0 \cdot 1 = 0 $$

 

Les vecteurs sont orthogonaux (perpendiculaires), et l’angle est \( \large 90^\circ \).

 

Exemple 2 :

 

$$ \large \mathbf{u} = (1,2), \; \mathbf{v} = (2,1) $$

$$ \large \mathbf{u} \cdot \mathbf{v} = 1 \cdot 2 + 2 \cdot 1 = 4 $$

 

Les longueurs sont \( \large |\mathbf{u}| = \sqrt{5}, \; |\mathbf{v}| = \sqrt{5} \). Donc :

 

$$ \large \cos(\theta) = \frac{4}{\sqrt{5} \cdot \sqrt{5}} = \frac{4}{5} $$

 

L’angle est donc :

 

$$ \large \theta = \cos^{-1}\left(\frac{4}{5}\right) \approx 36,9^\circ $$

 

 

Interprétation géométrique

Le produit scalaire mesure combien d’un vecteur pointe dans la même direction que l’autre. Si l’angle est aigu, le produit est positif. Si l’angle est obtus, le produit est négatif. Si l’angle est droit, le produit est nul.

 

 

Application

Le produit scalaire est utilisé en mathématiques et en physique pour déterminer des angles et pour savoir si des vecteurs sont perpendiculaires. En physique, il est aussi utilisé pour calculer la composante d’une force agissant dans une direction spécifique.