Varianz und Standardabweichung
Streuung
Die Streuung zeigt, wie stark die Beobachtungen um den Mittelwert variieren.
Wenn alle Beobachtungen nahe am Mittelwert liegen, ist die Streuung klein. Wenn sie weit entfernt sind, ist die Streuung groß.
Varianz
Die Varianz misst den durchschnittlichen quadrierten Abstand vom Mittelwert.
Um die Varianz zu berechnen, muss man:
- Von jeder Beobachtung den Mittelwert abziehen
- Die Differenzen quadrieren
- Den Durchschnitt der quadrierten Differenzen berechnen
$$ s^2 = \frac{(x_1 - \overline{x})^2 + (x_2 - \overline{x})^2 + ... + (x_n - \overline{x})^2}{n} $$
Standardabweichung
Die Standardabweichung ist die Quadratwurzel der Varianz. Sie gibt in derselben Einheit wie die Beobachtungen an, wie stark sie typischerweise vom Mittelwert abweichen.
$$ s = \sqrt{s^2} $$
Beispiel
Wir verwenden die Beobachtung der Körpergrößen der Schüler.
- Der Mittelwert ist \( \overline{x} = 164{,}8 \)
- Die Varianz ist \( s^2 = 40{,}36 \)
- Die Standardabweichung ist \( s \approx 6{,}35 \)
Das bedeutet, dass die Körpergrößen im Durchschnitt etwa 6,35 cm vom Mittelwert abweichen.
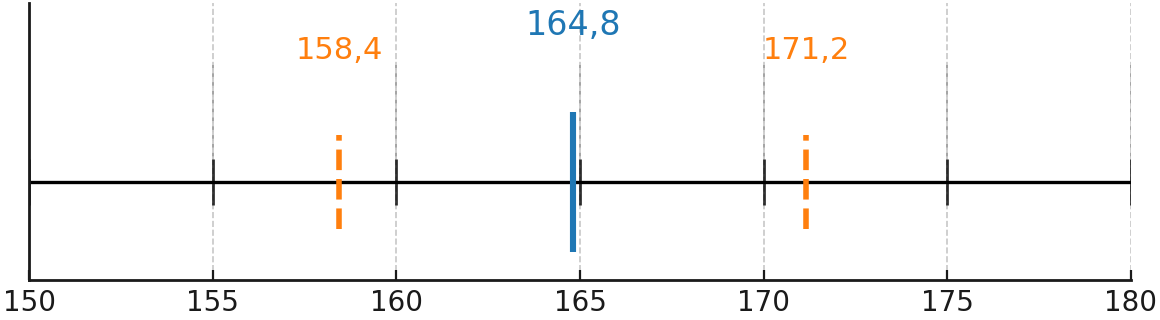
Diagramm
Die Standardabweichung kann in einem Diagramm dargestellt werden, in dem der Mittelwert markiert ist und die Intervalle \( \overline{x} \pm s \) angezeigt werden.