Volumen mit Vektoren

Das Volumen eines Körpers im Raum kann mithilfe von Vektoren berechnet werden. Besonders Parallelepipede (Quader) lassen sich in einer einfachen Formel ausdrücken, wenn sie durch drei Vektoren beschrieben werden.

 

Volumen eines Parallelepipeds

Für drei Vektoren \( \large \mathbf{u}, \mathbf{v}, \mathbf{w} \) im Raum gilt, dass das Volumen des von ihnen aufgespannten Parallelepipeds durch folgende Formel gegeben ist:

 

$$ \large V = \left| \det \begin{pmatrix} x_1 & x_2 & x_3 \\ y_1 & y_2 & y_3 \\ z_1 & z_2 & z_3 \end{pmatrix} \right| $$

 

wobei \( \large \mathbf{u} = (x_1,y_1,z_1) \), \( \large \mathbf{v} = (x_2,y_2,z_2) \) und \( \large \mathbf{w} = (x_3,y_3,z_3) \).

 

 

Beispiel

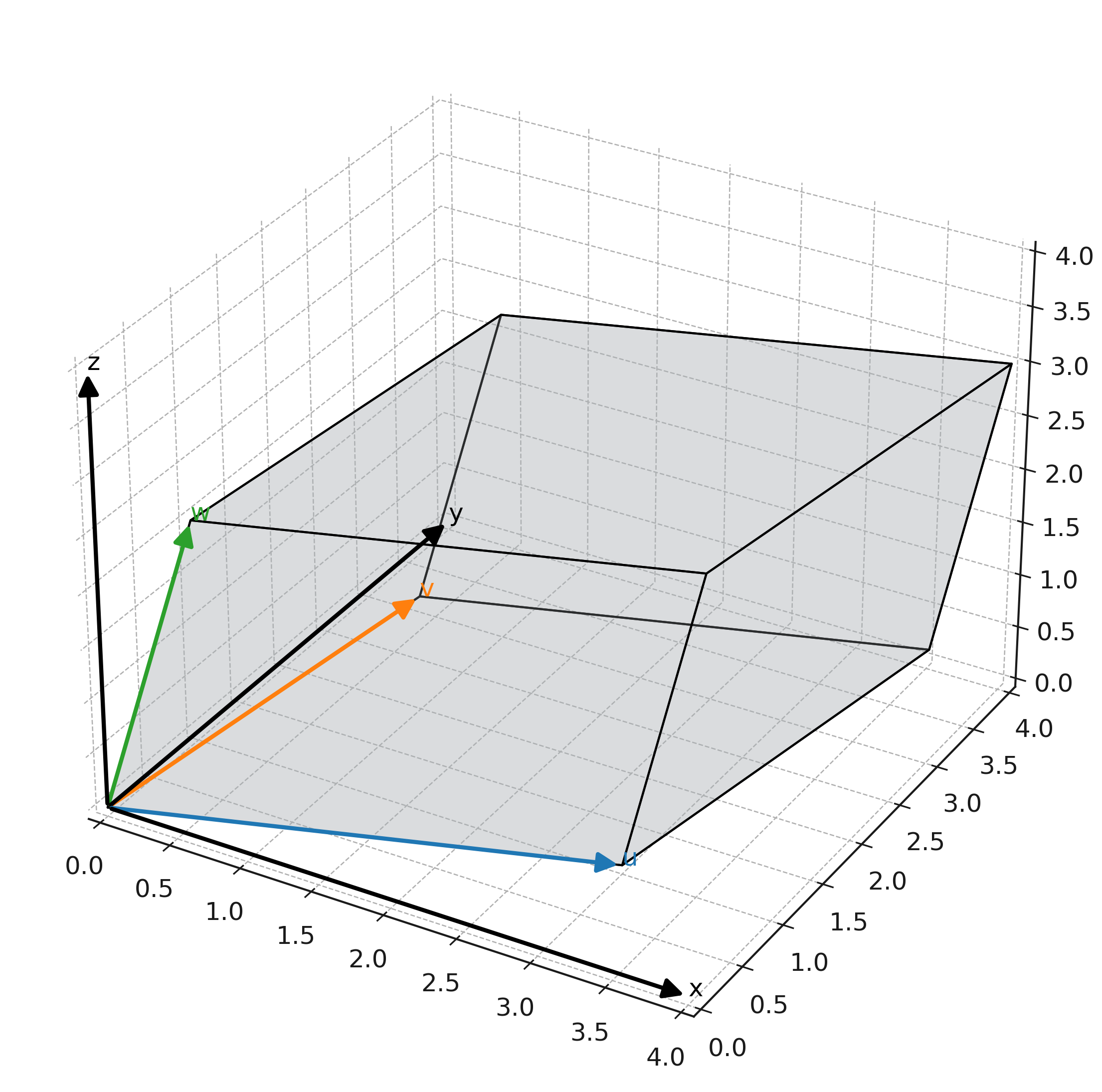
Wir nehmen \( \large \mathbf{u} = (3,1,0) \), \( \large \mathbf{v} = (1,2,1) \) und \( \large \mathbf{w} = (0,1,2) \).

 

$$ \large V = \left| \det \begin{pmatrix} 3 & 1 & 0 \\ 1 & 2 & 1 \\ 0 & 1 & 2 \end{pmatrix} \right| $$

 

Bei der Berechnung einer Determinante kann man sie nach einer beliebigen Zeile oder Spalte entwickeln. Das Ergebnis ist immer dasselbe, unabhängig von der Wahl. Zur Vereinfachung entwickeln wir hier nach der ersten Zeile.

 

$$ \large V= 3 \cdot \det \begin{pmatrix} 2 & 1 \\ 1 & 2 \end{pmatrix} - 1 \cdot \det \begin{pmatrix} 1 & 1 \\ 0 & 2 \end{pmatrix} + 0 \cdot \det \begin{pmatrix} 1 & 2 \\ 0 & 1 \end{pmatrix} $$

 

Die kleinen Determinanten werden jeweils einzeln berechnet:

$$ \large \det \begin{pmatrix} 2 & 1 \\ 1 & 2 \end{pmatrix} = 2 \cdot 2 - 1 \cdot 1 = 3 $$

$$ \large \det \begin{pmatrix} 1 & 1 \\ 0 & 2 \end{pmatrix} = 1 \cdot 2 - 1 \cdot 0 = 2 $$

 

Wir setzen die Ergebnisse nun wieder in den Ausdruck ein:

 

$$ \large V = | 3 \cdot 3 - 1 \cdot 2 + 0 | = | 9 - 2 | = | 7 | = 7 $$

 

Das Volumen des Parallelepipeds beträgt also 7. Wir verwenden den Absolutwert, weil eine Determinante je nach Orientierung der Vektoren negativ sein kann, das Volumen jedoch niemals kleiner als null ist.

 

 

Geometrische Interpretation

Die Formel entspricht der Berechnung Grundfläche mal Höhe. Die Grundfläche wird über eine Flächenberechnung ermittelt, und die Höhe erhält man durch die senkrechte Projektion des dritten Vektors auf die Grundfläche.

 

Anwendung

Volumenformeln mit Vektoren werden in Geometrie, Linearer Algebra und Physik verwendet. Sie ermöglichen die Berechnung des Volumens von Quadern und anderen Körpern in Koordinatensystemen und bilden die Grundlage für weitere Themen wie Determinanten, Kreuzprodukt und Integrale.