Skalarprodukt

Das Skalarprodukt ist eine Operation zwischen zwei Vektoren, die eine Zahl ergibt. Es wird verwendet, um Winkel zwischen Vektoren zu berechnen und um festzustellen, ob sie senkrecht aufeinander stehen.

 

Definition

Für zwei Vektoren im Raum \( \large \mathbf{u} = (x_1,y_1,z_1) \) und \( \large \mathbf{v} = (x_2,y_2,z_2) \) ist das Skalarprodukt definiert als

 

$$ \large \mathbf{u} \cdot \mathbf{v} = x_1x_2 + y_1y_2 + z_1z_2 $$

 

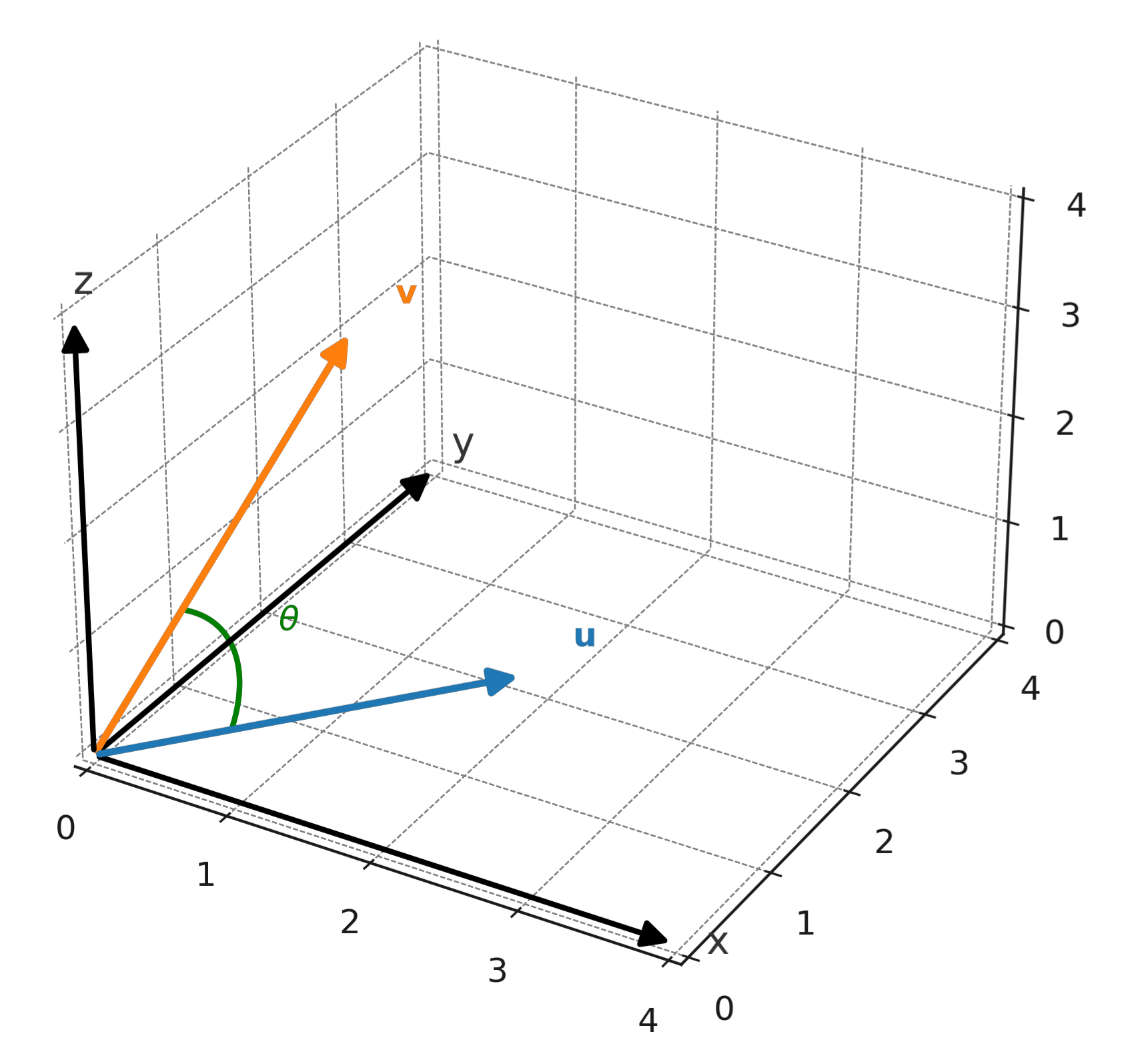
Eine andere Formel zeigt den Zusammenhang mit dem Winkel zwischen den Vektoren:

 

$$ \large \mathbf{u} \cdot \mathbf{v} = |\mathbf{u}| \cdot |\mathbf{v}| \cdot \cos(\theta) $$

 

wobei \( \large \theta \) der Winkel zwischen \( \large \mathbf{u} \) und \( \large \mathbf{v} \) ist.

 

 

Beispiel

Wir nehmen \( \large \mathbf{u} = (1,2,3) \) und \( \large \mathbf{v} = (4,-1,2) \).

 

$$ \large \mathbf{u} \cdot \mathbf{v} = 1 \cdot 4 + 2 \cdot (-1) + 3 \cdot 2 = 4 - 2 + 6 = 8 $$

 

Das Skalarprodukt ist 8.

 

 

Geometrische Interpretation

Das Skalarprodukt misst, wie stark die beiden Vektoren in dieselbe Richtung zeigen. Ist der Winkel kleiner als 90°, ist das Skalarprodukt positiv. Ist der Winkel größer als 90°, ist es negativ. Sind die Vektoren senkrecht, ist das Skalarprodukt null.

 

 

Anwendung

Das Skalarprodukt wird in vielen Zusammenhängen verwendet, unter anderem zur Bestimmung von Winkeln zwischen Vektoren, zur Feststellung der Orthogonalität und in der Physik zur Berechnung der Arbeit, die eine Kraft entlang einer Bewegung verrichtet.