Geraden und Ebenen im Raum

Im Raum können Geraden und Ebenen mithilfe von Vektoren beschrieben werden. Dies ermöglicht es, systematisch mit Geometrie in drei Dimensionen zu arbeiten.

 

Geraden

Eine Gerade im Raum kann durch einen Punkt \( \large \mathbf{a} \) und einen Richtungsvektor \( \large \mathbf{r} \) beschrieben werden. Alle Punkte \( \large \mathbf{x} \) auf der Geraden können geschrieben werden als

 

$$ \large \mathbf{x} = \mathbf{a} + t \cdot \mathbf{r}, \quad t \in \mathbb{R} $$

 

Hierbei ist \( \large t \) ein Parameter, der bestimmt, wie weit man sich entlang der Geraden bewegt.

 

Beispiel

Eine Gerade durch den Punkt \( \large (1,2,0) \) mit Richtungsvektor \( \large (2,-1,3) \) ist gegeben durch:

 

$$ \large \mathbf{x} = (1,2,0) + t \cdot (2,-1,3) $$

 

Ebenen

Eine Ebene kann durch einen Punkt \( \large \mathbf{a} \) und einen Normalenvektor \( \large \mathbf{n} \) beschrieben werden. Alle Punkte \( \large \mathbf{x} \) in der Ebene erfüllen

 

$$ \large (\mathbf{x} - \mathbf{a}) \cdot \mathbf{n} = 0 $$

 

Das bedeutet, dass die Differenz zwischen einem beliebigen Punkt der Ebene und dem Punkt \( \large \mathbf{a} \) senkrecht zum Normalenvektor steht.

 

Beispiel

Eine Ebene durch den Punkt \( \large (1,0,2) \) mit Normalenvektor \( \large (2,-1,1) \) kann beschrieben werden als

 

$$ \large 2(x-1) -1(y-0) + 1(z-2) = 0 $$

 

oder umgeschrieben:

 

$$ \large 2x - y + z = 4 $$

 

Geometrische Interpretation

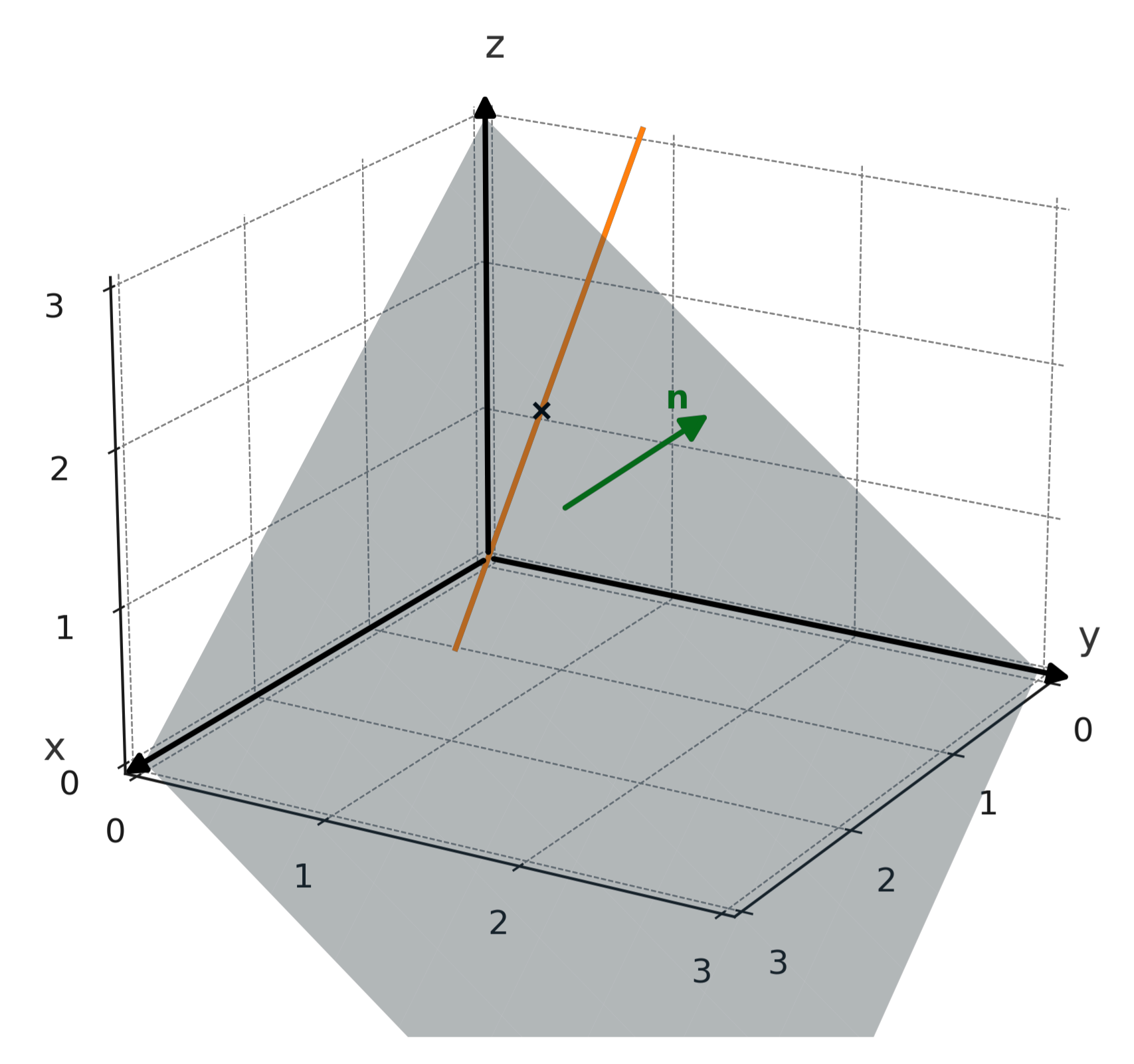
Eine Gerade beschreibt alle Punkte entlang einer Richtung, während eine Ebene alle Punkte in einer unendlichen „flachen Schicht“ beschreibt. Der Normalenvektor (n) einer Ebene steht senkrecht auf dieser Fläche.

 

Der Schnittpunkt zwischen einer Geraden und einer Ebene kann ein einzelner Punkt sein, der im untenstehenden Bild mit einem Kreuz markiert ist.

Er kann auch die gesamte Gerade sein, wenn die Gerade in der Ebene liegt, oder leer, wenn die Gerade parallel und außerhalb der Ebene verläuft.

 

 

Anwendung

Geraden und Ebenen im Raum sind zentral in Geometrie, Physik und Informatik. Sie werden z. B. verwendet, um Bewegungsbahnen, Spiegelungen, 3D-Modellierung und Kollisionsdetektion in der Computergrafik zu beschreiben.