Koordinaten im 3D-Raum

Im 3D-Raum wird ein Punkt durch drei Koordinaten beschrieben. Während wir in der Ebene zwei Zahlen verwenden, um eine Position anzugeben, sind im Raum drei Zahlen erforderlich, um einen Punkt eindeutig zu bestimmen.

 

Definition

Ein Punkt \( \large P \) im Raum wird angegeben als

 

$$ \large P = (x,y,z) $$

 

Hier ist \( \large x \) der Abstand entlang der x-Achse, \( \large y \) der Abstand entlang der y-Achse und \( \large z \) der Abstand entlang der z-Achse.

 

 

Beispiel

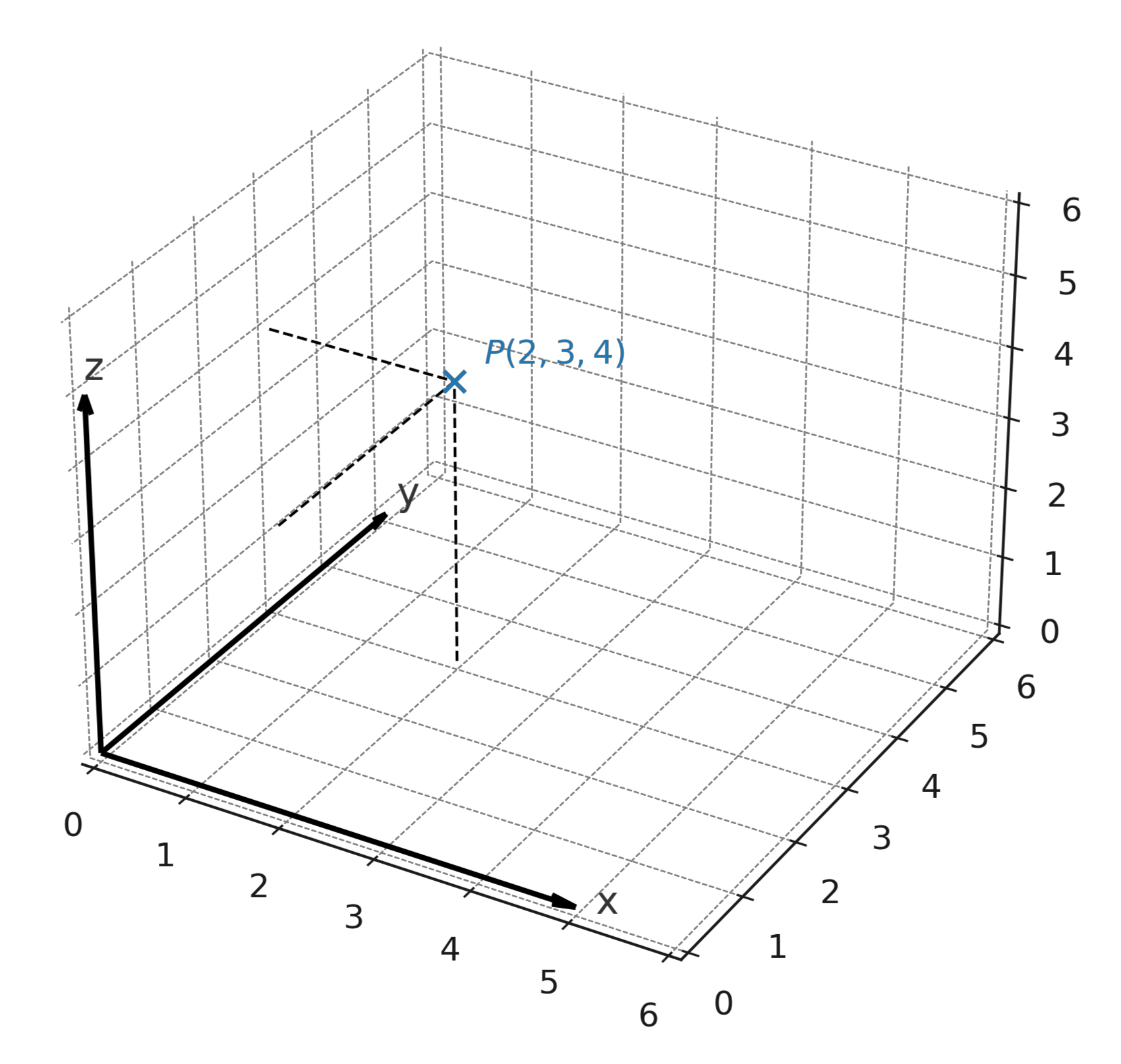
Der Punkt \( \large P = (2,3,4) \) bedeutet, dass man 2 Einheiten entlang der x-Achse, 3 Einheiten entlang der y-Achse und 4 Einheiten nach oben entlang der z-Achse geht.

 

 

Koordinatenachsen und Ursprung

Die drei Achsen heißen x-, y- und z-Achse. Ihr gemeinsamer Ausgangspunkt heißt Ursprung und hat die Koordinaten

 

$$ \large O = (0,0,0) $$

 

Ein Vektor vom Ursprung zu einem Punkt \( \large P=(x,y,z) \) wird geschrieben als

 

$$ \large \vec{OP} = (x,y,z) $$

 

 

Abstand im Raum

Der Abstand vom Ursprung zu einem Punkt \( \large (x,y,z) \) wird durch die Erweiterung des Satzes des Pythagoras gefunden:

 

$$ \large |(x,y,z)| = \sqrt{x^2 + y^2 + z^2} $$

 

Dies ist die Länge des Vektors vom Ursprung zu dem Punkt.

 

 

Geometrische Interpretation

Ein Koordinatensystem im Raum wird aus drei zueinander senkrechten Achsen aufgebaut. Jeder Punkt kann als eine Ecke eines rechteckigen Prismas mit dem Ursprung als Ausgangspunkt gesehen werden.

 

 

Anwendung

Koordinaten im 3D-Raum werden überall in Mathematik, Physik und Informatik verwendet, zum Beispiel um Punkte in der Geometrie, Positionen im Raum oder Objekte in 3D-Grafiken zu beschreiben.