Kreuzprodukt
Das Kreuzprodukt zweier Vektoren im Raum ist ein Vektor, der senkrecht auf beiden ursprünglichen Vektoren steht. Das Kreuzprodukt wird verwendet, um Flächen, Normalvektoren und Orientierungen in der 3D-Geometrie zu bestimmen.
Definition
Für zwei Vektoren \( \large \mathbf{u} = (x_1,y_1,z_1) \) und \( \large \mathbf{v} = (x_2,y_2,z_2) \) ist das Kreuzprodukt durch die Determinante definiert:
$$ \large \mathbf{u} \times \mathbf{v} = \begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ x_1 & y_1 & z_1 \\ x_2 & y_2 & z_2 \end{vmatrix} = (y_1z_2 - z_1y_2,\; z_1x_2 - x_1z_2,\; x_1y_2 - y_1x_2) $$
Beispiel
Wir nehmen \( \large \mathbf{u} = (1,2,3) \) und \( \large \mathbf{v} = (4,5,6) \).
$$ \large \mathbf{u} \times \mathbf{v} = \begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ 1 & 2 & 3 \\ 4 & 5 & 6 \end{vmatrix} = (-3,6,-3) $$
Das Ergebnis ist ein neuer Vektor \( \large (-3,6,-3) \), der senkrecht sowohl auf \( \large \mathbf{u} \) als auch auf \( \large \mathbf{v} \) steht.
Geometrische Interpretation
Die Länge des Kreuzprodukts entspricht der Fläche des Parallelogramms, das von den Vektoren aufgespannt wird:
$$ \large |\mathbf{u} \times \mathbf{v}| = |\mathbf{u}| \cdot |\mathbf{v}| \cdot \sin(\theta) $$
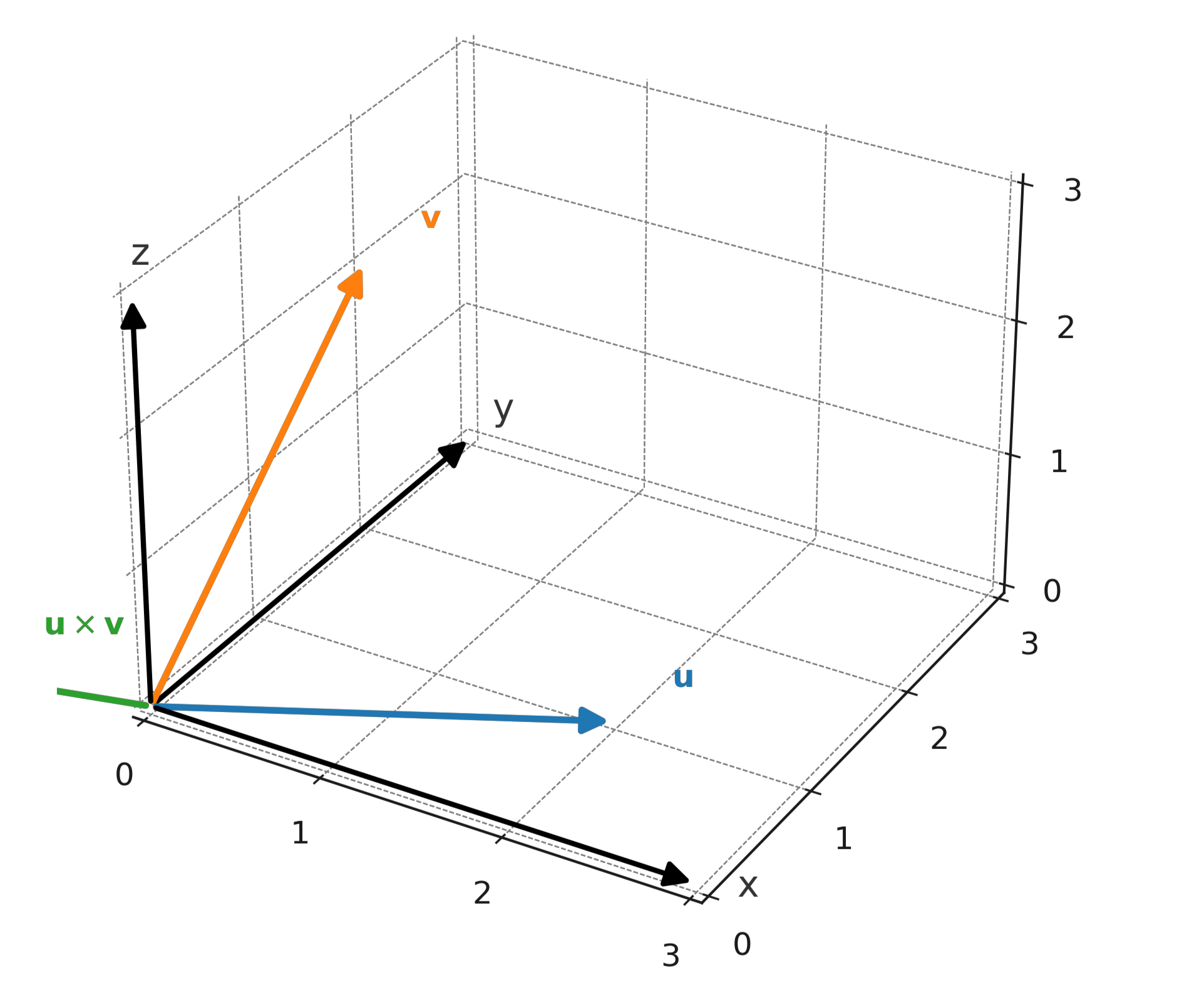
Die Richtung wird durch die Rechte-Hand-Regel bestimmt: Wenn man den Zeigefinger der rechten Hand in Richtung von \( \large \mathbf{u} \) und den Mittelfinger in Richtung von \( \large \mathbf{v} \) zeigt, dann zeigt der Daumen in Richtung von \( \large \mathbf{u} \times \mathbf{v} \).
Anwendung
Das Kreuzprodukt wird in vielen Bereichen der Mathematik und Physik verwendet:
- Um einen Normalvektor zu einer Ebene zu finden
- Um die Fläche von Parallelogrammen und Dreiecken in 3D zu berechnen
- In der Mechanik zur Bestimmung des Moments einer Kraft
- In der Computergrafik zur Berechnung der Orientierung von Flächen