Mængdeoperationer
Mængdeoperationer er metoder til at kombinere eller sammenligne mængder. Her ser vi på union, fællesmængde (snit), disjunkte mængder, differens, komplementærmængder og hvordan disse kan visualiseres med Venn-diagrammer.
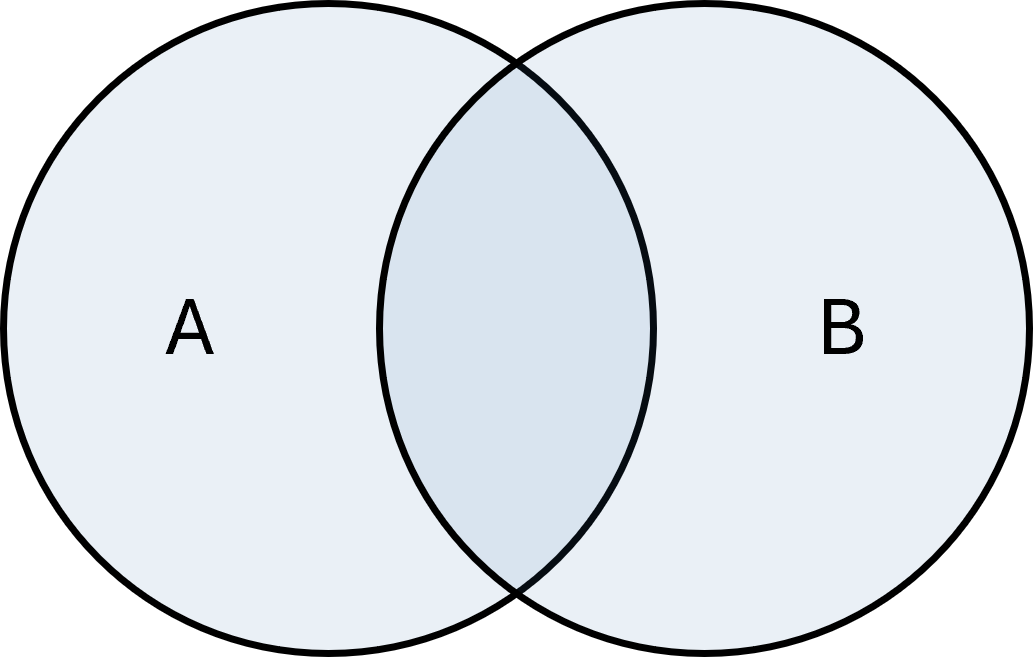
Union
Unionen af to mængder \( \large A\) og \( \large B\) er mængden af alle elementer, der er i enten \( \large A\) eller \( \large B\) (eller begge). Det skrives som:
$$ \large A \cup B = \{x \mid x \in A \;\vee\; x \in B\} $$
Eksempel: Hvis \( \large A = \{1,2,3\}\) og \( \large B = \{3,4,5\}\), så er \( \large A \cup B = \{1,2,3,4,5\}\).
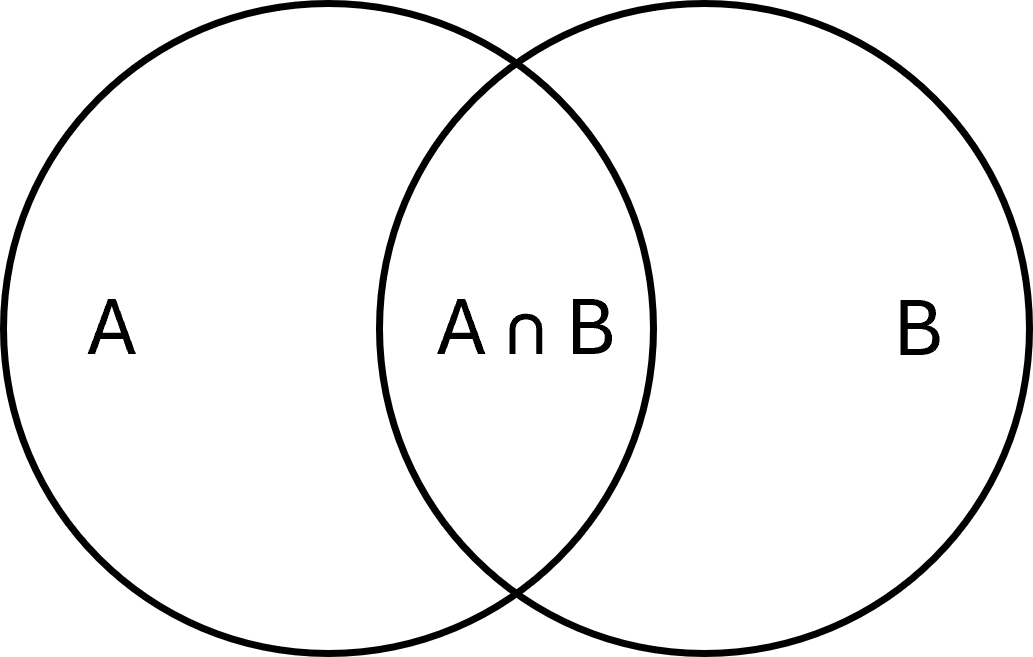
Fællesmængde (Snit)
Fællesmængden af to mængder er de elementer, som de har tilfælles. Det skrives som:
$$ \large A \cap B = \{x \mid x \in A \;\wedge\; x \in B\} $$
Eksempel: Hvis \( \large A = \{1,2,3\}\) og \( \large B = \{3,4,5\}\), så er \( \large A \cap B = \{3\}\).
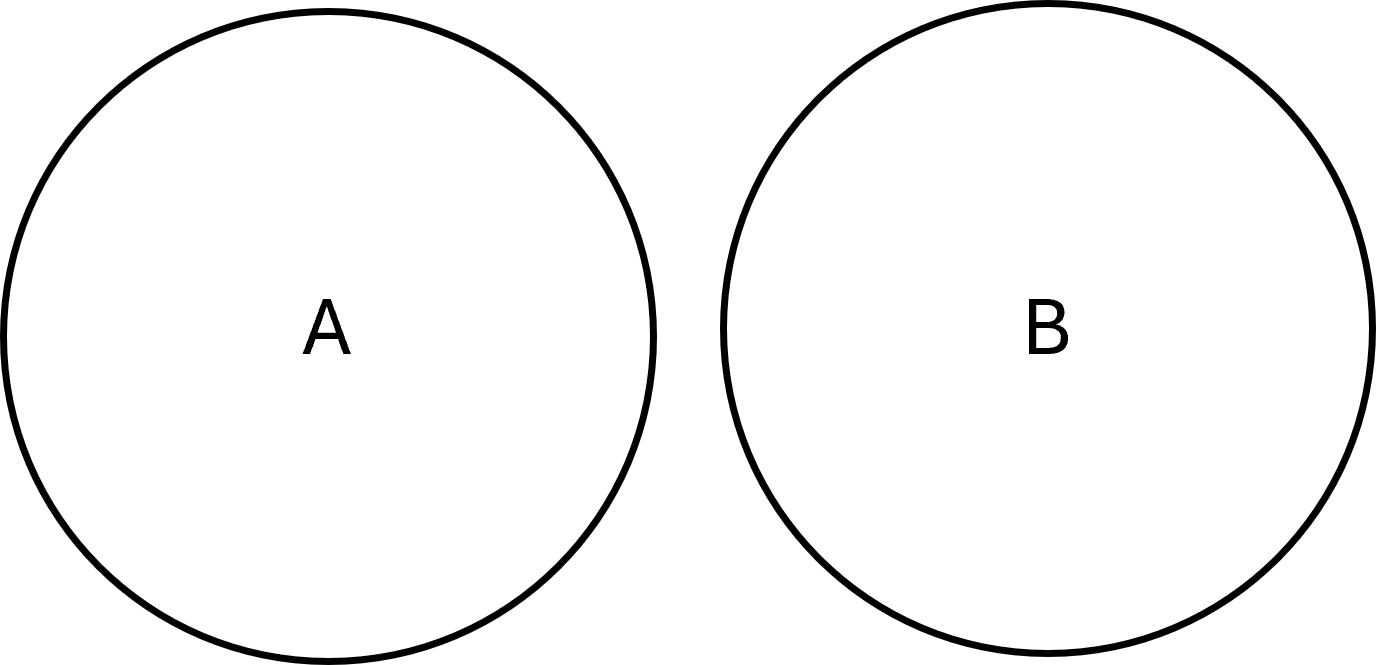
Disjunkte mængder
To mængder er disjunkte, hvis de ikke har nogen fælles elementer. Det vil sige, at deres snit er tomt:
$$ \large A \cap B = \emptyset $$
Eksempel: \( \large A = \{1,2,3\}, B = \{4,5,6\}\).
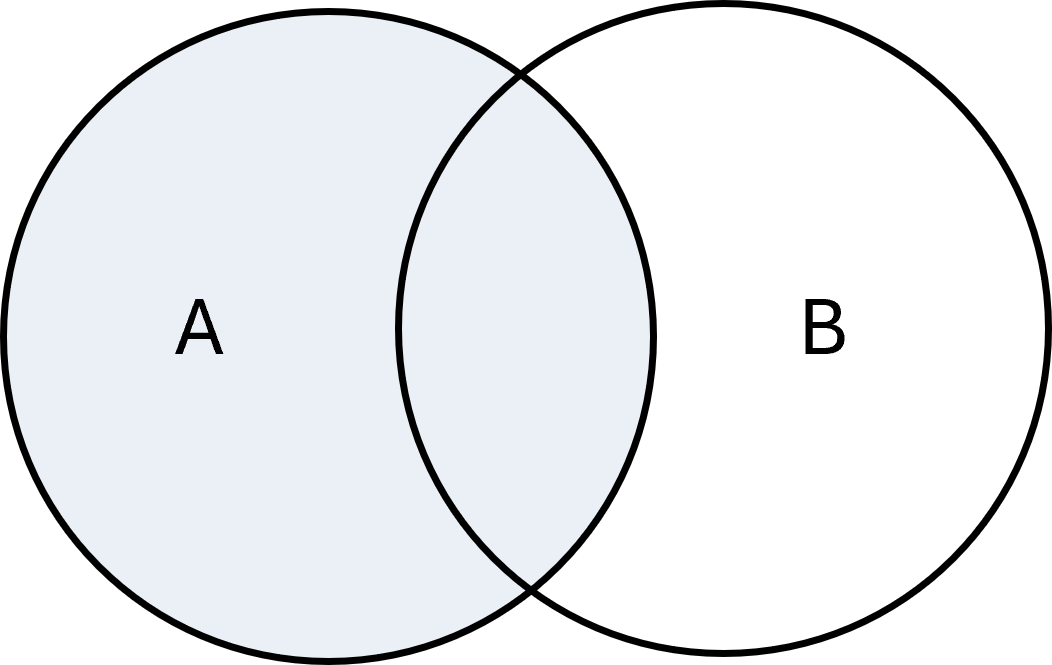
Differens
Differensen af to mængder \( \large A\) og \( \large B\), skrevet som \( \large A - B\) eller \( \large A \setminus B\), er de elementer, der er i \( \large A\), men ikke i \( \large B\):
$$ \large A - B = \{x \mid x \in A \;\wedge\; x \notin B\} $$
Eksempel: Hvis \( \large A = \{1,2,3\}, B = \{3,4,5\}\), så er \( \large A - B = \{1,2\}\).
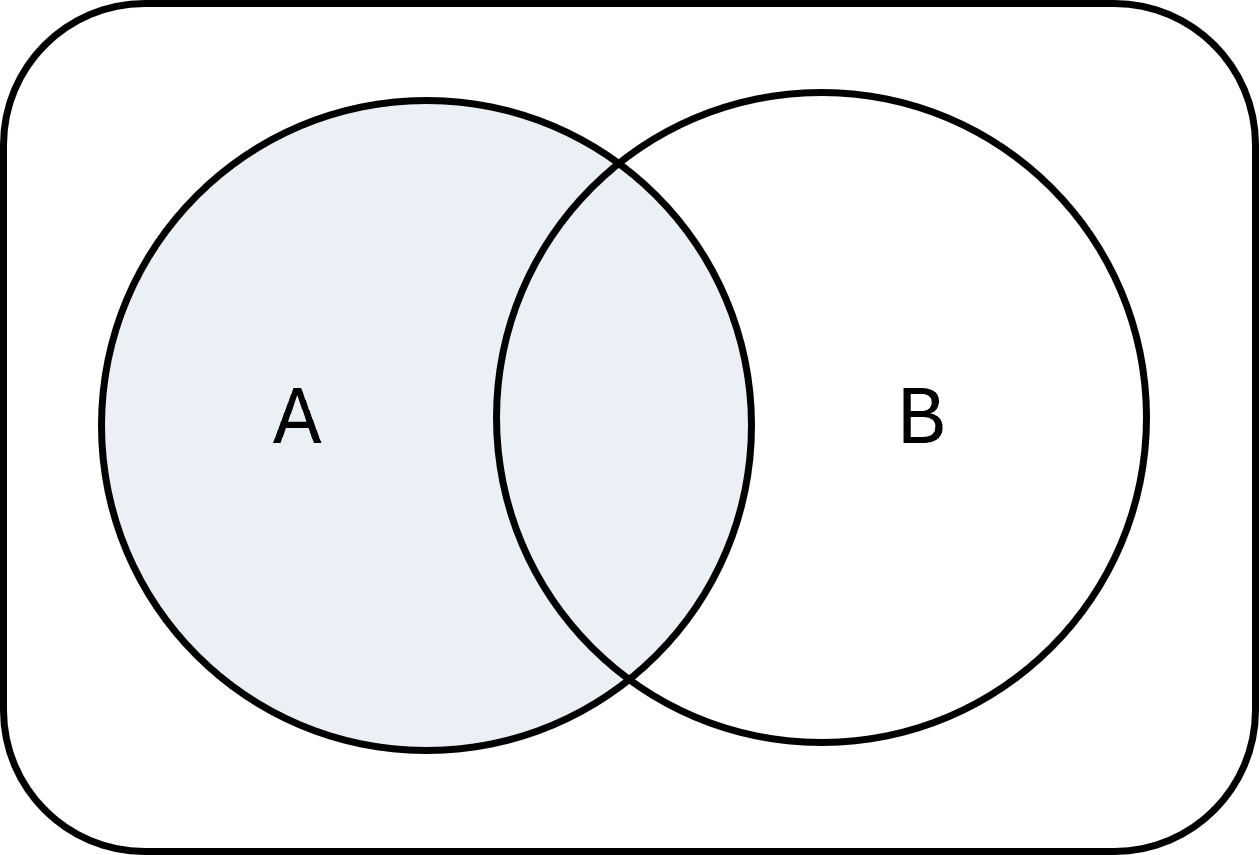
Komplementærmængde
Hvis vi har et univers \( \large U\), der indeholder alle mulige elementer, kan vi definere komplementæret til en mængde \( \large A\) som alle de elementer i \( \large U\), der ikke er i \( \large A\). Det skrives som:
$$ \large A^{c} = \{x \in U \mid x \notin A\} $$
Eksempel: Hvis \( \large U = \{1,2,3,4,5\}\) og \( \large A = \{1,2\}\), så er \( \large A^{c} = \{3,4,5\}\).
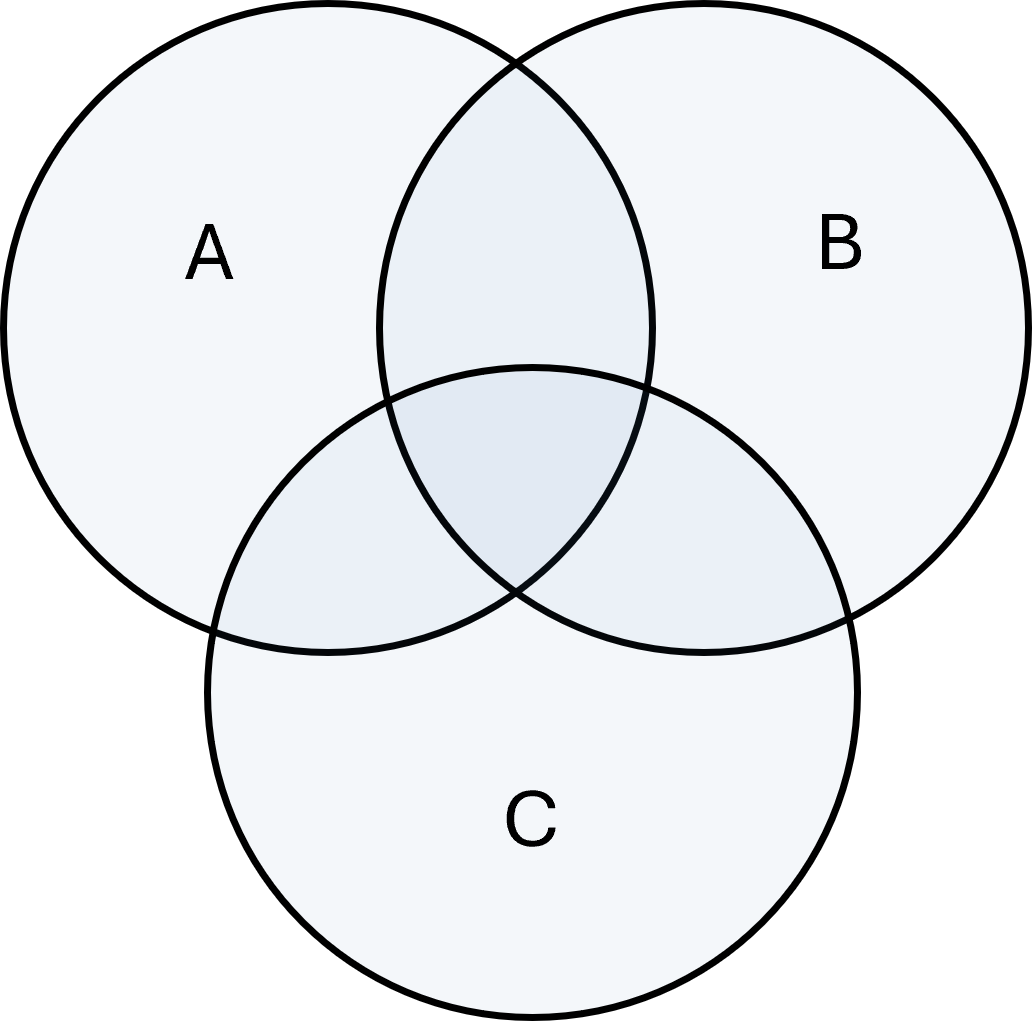
Venn-diagrammer
Venn-diagrammer bruges ofte til at illustrere mængdeoperationer grafisk.
Cirkler repræsenterer mængder, og overlappende områder viser, hvordan union, snit, differens og komplement fungerer.