En vigtig del af mængdelæren handler om at sammenligne og kombinere mængder. Her ser vi på delmængder, ægte delmængder, fællesmængder, potensmængder og det kartesiske produkt.

 

Delmængde

En mængde \( \large A\) er en delmængde af en anden mængde \( \large B\), hvis alle elementer i \( \large A\) også findes i \( \large B\). Det skrives som:

 

$$ \large A \subseteq B $$

 

 

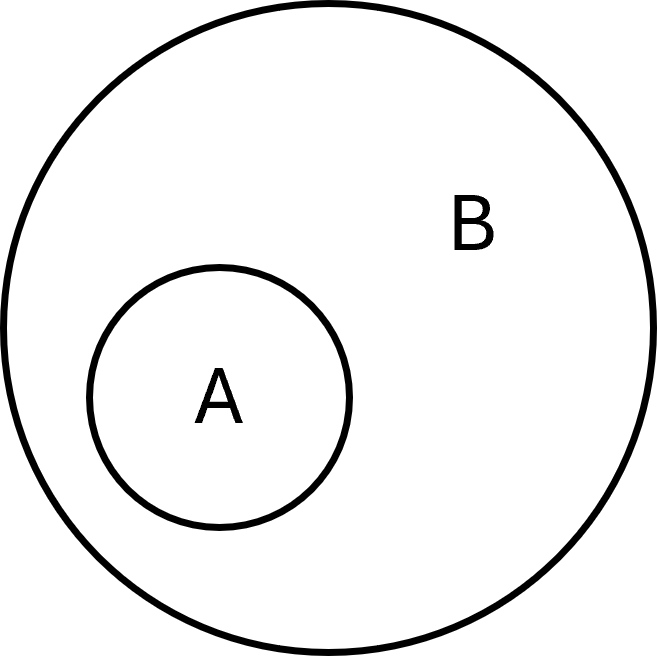
Formelt kan det defineres sådan:

 

$$ \large A \subseteq B \;\;\Leftrightarrow\;\; \forall x \in A \Rightarrow x \in B $$

 

Eksempler:

 

• \( \large \{1,2\} \subseteq \{1,2,3,4\}\)
• Den tomme mængde er altid en delmængde: \( \large \emptyset \subseteq A\) for enhver mængde \( \large A\).

 

Bemærk: I nogle bøger bruges symbolet \( \large \subset\) i stedet for \( \large \subseteq\) til at betegne delmængder. Her bruger vi \( \large \subseteq\) som standard.

 

 

Ægte delmængde

En mængde \( \large A\) er en ægte delmængde af \( \large B\), hvis \( \large A \subseteq B\), men \( \large A \neq B\).

Det betyder, at \( \large B\) indeholder mindst ét element, som ikke er i \( \large A\).

Notationen er:

 

$$ \large A \subset B $$

 

Eksempel: \( \large \{1,2\} \subset \{1,2,3\}\).

 

 

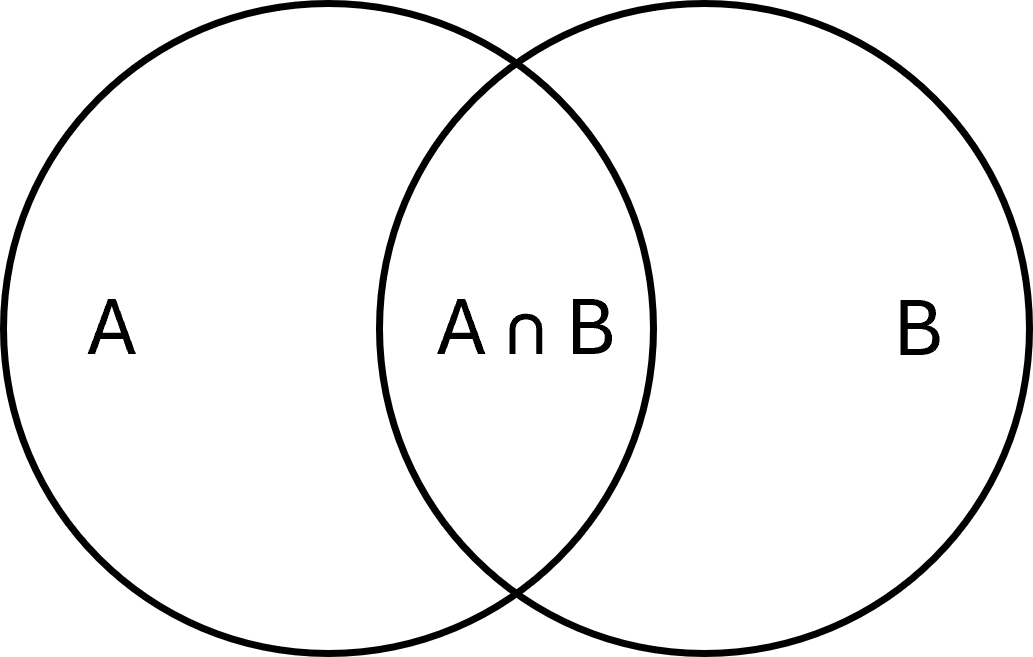
Fællesmængde

Fællesmængden (eller snittet) af to mængder \( \large A\) og \( \large B\) er mængden af de elementer, der er i begge mængder. Det skrives som:

 

$$ \large A \cap B = \{x \mid x \in A \;\wedge\; x \in B\} $$

 

Eksempel: Hvis \( \large A = \{1,2,3\}\) og \( \large B = \{3,4,5\}\), så er \( \large A \cap B = \{3\}\).

 

 

 

 

Potensmængde

Potensmængden til en mængde \( \large A\) er mængden af alle delmængder af \( \large A\).

Potensmængden skrives som \( \large \mathcal{P}(A)\).

 

Hvis \( \large A = \{0,1\}\), så er:

 

$$ \large \mathcal{P}(A) = \{\emptyset, \{0\}, \{1\}, \{0,1\}\} $$

 

Antallet af elementer i en potensmængde er \( \large 2^{|A|}\).

For eksempel, hvis \( \large |A| = 3\), så har \( \large \mathcal{P}(A)\) \( \large 2^3 = 8\) elementer.

 

 

Kartesisk produkt

Det kartesiske produkt af to mængder \( \large A\) og \( \large B\) er mængden af alle ordnede par, hvor første komponent kommer fra \( \large A\) og anden komponent fra \( \large B\).

Det skrives som:

 

$$ \large A \times B = \{(a,b) \mid a \in A \;\wedge\; b \in B\} $$

 

Eksempel: Hvis \( \large A = \{1,2\}\) og \( \large B = \{a,b\}\), så er:

 

$$ \large A \times B = \{(1,a),(1,b),(2,a),(2,b)\} $$

 

Bemærk at rækkefølgen betyder noget: \( \large A \times B \neq B \times A\) i almindelighed.