Kartesisk produkt i to og flere dimensioner

Det kartesiske produkt er en måde at kombinere mængder på for at danne ordnede par eller tuples. Navnet kommer fra den franske matematiker René Descartes (latin: Cartesius), fordi begrebet ligger til grund for koordinatsystemer og geometrisk repræsentation af punkter.

 

 

Kartesisk produkt af to mængder

Hvis vi har to mængder \( \large A\) og \( \large B\), er deres kartesiske produkt mængden af alle ordnede par, hvor første element kommer fra \( \large A\) og andet element fra \( \large B\):

 

$$ \large A \times B = \{(a,b) \mid a \in A, \; b \in B\} $$

 

Eksempel: Lad \( \large A = \{1,2\}\) og \( \large B = \{x,y\}\). Da er:

 

$$ \large A \times B = \{(1,x), (1,y), (2,x), (2,y)\} $$

 

 

 

 

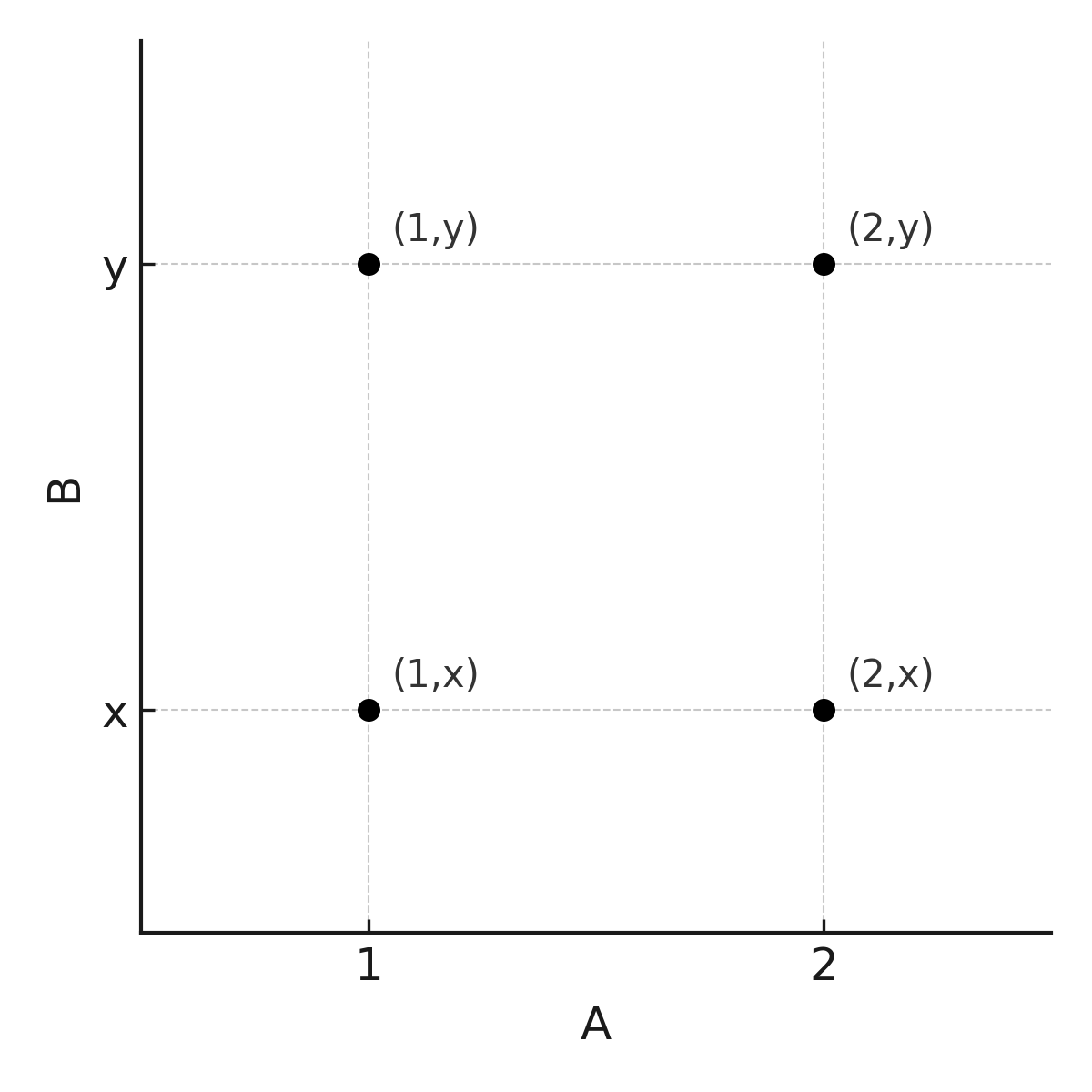
Bemærk: Rækkefølgen betyder noget. Mængden \( \large B \times A\) er:

 

$$ \large B \times A = \{(x,1),(x,2),(y,1),(y,2)\} $$

 

Altså gælder i almindelighed: \( \large A \times B \neq B \times A\).

 

Kardinaliteten (antal elementer) i produktet bestemmes af:

 

$$ \large |A \times B| = |A| \cdot |B| $$

 

Eksempel: Hvis \( \large |A|=3\) og \( \large |B|=4\), så indeholder \( \large A \times B\) \( \large 3 \cdot 4 = 12\) ordnede par.

 

 

Kartesisk produkt i flere dimensioner

Idéen kan udvides til tre eller flere mængder. For tre mængder defineres:

 

$$ \large A \times B \times C = \{(a,b,c) \mid a \in A, \; b \in B, \; c \in C\} $$

 

Eksempel: Hvis \( \large A = \{1,2\}, B = \{x\}, C = \{p,q\}\), da er:

 

$$ \large A \times B \times C = \{(1,x,p), (1,x,q), (2,x,p), (2,x,q)\} $$

 

Generelt kan man definere et kartesisk produkt af \( \large n\) mængder, som indeholder alle \( \large n\)-tuples, hvor hvert element kommer fra en af mængderne. Skrives alle mængderne ens, fx \( \large A \times A \times \cdots \times A\) (med \( \large n\) gentagelser), noteres det som \( \large A^n\).

 

Eksempler:

 

• \( \large \mathbb{R}^2\): alle punkter i planen, skrevet som \((x,y)\).
• \( \large \mathbb{R}^3\): alle punkter i rummet, skrevet som \((x,y,z)\).
• \( \large \{0,1\}^3\): alle binære triples, dvs. \( \large (0,0,0),(0,0,1),\ldots,(1,1,1)\).

 

Antallet af elementer i et kartesisk produkt af endelige mængder er:

 

$$ \large |A_1 \times A_2 \times \cdots \times A_n| = |A_1| \cdot |A_2| \cdot \ldots \cdot |A_n| $$

 

 

Betydning og anvendelser

Kartesiske produkter giver en systematisk måde at bygge nye strukturer ud fra kendte mængder.

De er grundlaget for:

 

• Koordinatsystemer i matematik og geometri.
• Tabeller og datastrukturer i informatik.
• Relationer mellem objekter (fx grafer).