Bestemt integral

Det bestemte integral bruges til at beregne den samlede størrelse af en funktion mellem to punkter. Hvor det ubestemte integral beskriver alle stamfunktioner, giver det bestemte integral et tal, der repræsenterer den akkumulerede værdi — ofte et areal.

 

 

Definition

Det bestemte integral af en funktion \( \large f(x) \) fra \( \large a \) til \( \large b \) defineres som grænsen for summen af mange små rektangler under grafen:

 

$$ \large \int_a^b f(x)\,dx \;=\; \lim_{n \to \infty} \sum_{i=1}^{n} f(x_i)\,\Delta x $$

 

Hvert led i summen repræsenterer arealet af et lille rektangel med højde \( \large f(x_i) \) og bredde \( \large \Delta x \). Når antallet af rektangler øges, bliver tilnærmelsen mere præcis, og i grænsen fås det nøjagtige areal.

 

 

Geometrisk fortolkning

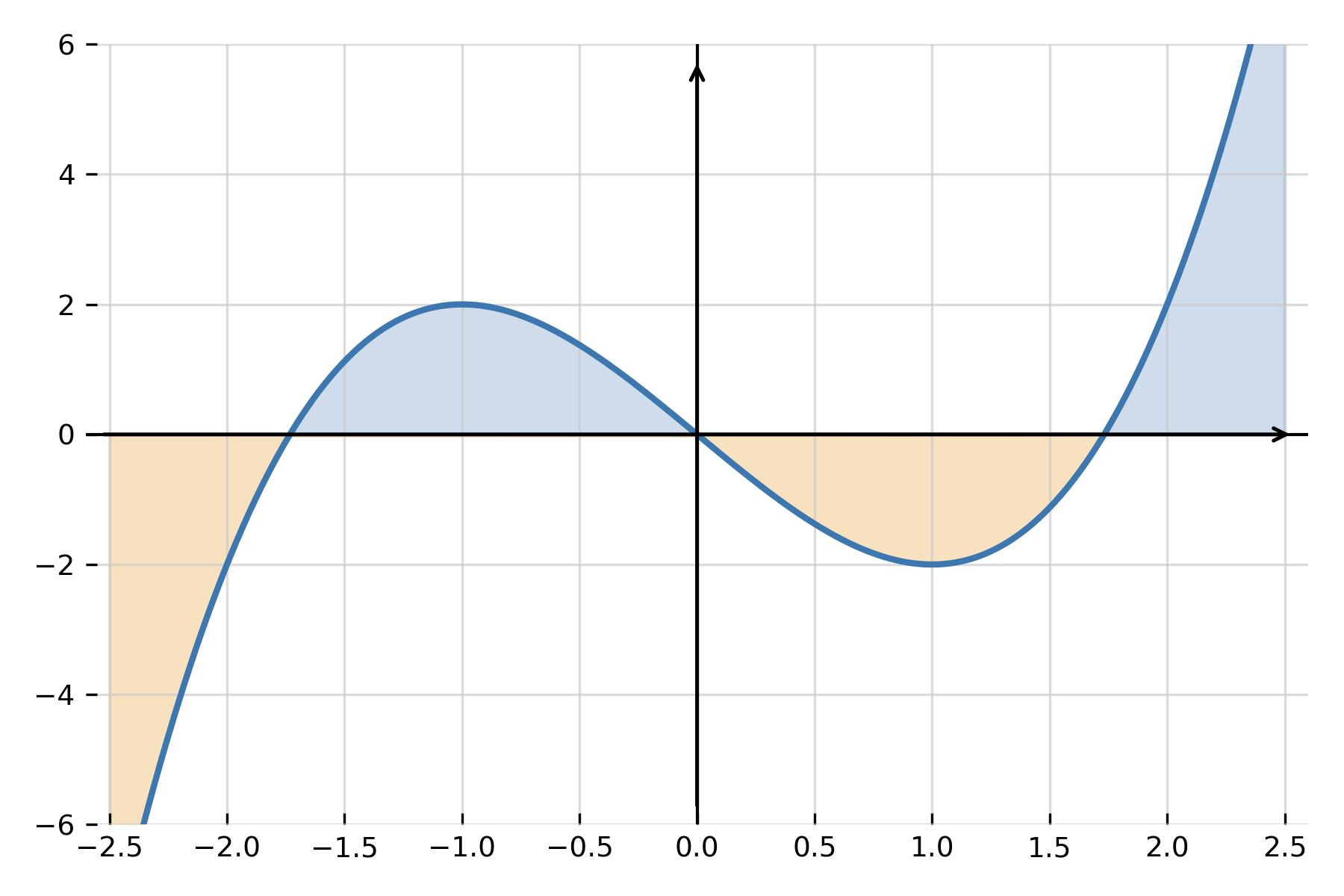
Hvis \( \large f(x) \ge 0 \) i intervallet, repræsenterer det bestemte integral arealet mellem grafen og x-aksen. Hvis funktionen krydser x-aksen, tælles områder under aksen negativt, så integralet viser nettoarealet.

 

 

 

Fundamentalsætningen

Der er en tæt sammenhæng mellem stamfunktioner og bestemte integraler. Hvis \( \large F \) er en stamfunktion til \( \large f \), gælder den fundamentale sætning i integralregningen:

 

$$ \large \int_a^b f(x)\,dx \;=\; F(b) - F(a) $$

 

Det betyder, at man kan finde et bestemt integral uden at beregne Riemann-summer. I stedet findes en stamfunktion, og man trækker funktionsværdierne ved de to grænser fra hinanden.

 

 

Eksempel 1: Areal under grafen

Find arealet under \( \large f(x) = x^2 \) fra \( \large x=0 \) til \( \large x=3 \):

 

$$ \large \int_0^3 x^2\,dx \;=\; \Big[\tfrac{1}{3}x^3\Big]_0^3 \;=\; \tfrac{1}{3}\cdot 27 - 0 \;=\; 9 $$

 

Arealet under grafen er altså 9 enheder.

 

 

Eksempel 2: Negativt og positivt bidrag

Find \( \large \int_{-1}^{2} (x-1)\,dx \):

 

$$ \large \int_{-1}^{2} (x-1)\,dx \;=\; \Big[\tfrac{1}{2}x^2 - x\Big]_{-1}^{2} \;=\; \big(2 - 2\big) - \big(\tfrac{1}{2} - (-1)\big) = -\tfrac{3}{2} $$

 

Integralet er negativt, fordi funktionen ligger under x-aksen i en del af intervallet. Det bestemte integral måler altså netto-akkumulationen, ikke blot summen af positive arealer.

 

 

Fortegn og akkumuleret størrelse

Et positivt integral betyder, at funktionen i gennemsnit ligger over x-aksen i intervallet. Et negativt integral betyder det modsatte. I fysik og økonomi tolkes dette som overskud eller underskud i en samlet størrelse.

 

 

Grafisk fortolkning

Det bestemte integral kan opfattes som summen af arealer med fortegn. Derfor kan man visualisere det som arealet mellem grafen og x-aksen, hvor arealer under aksen trækkes fra.

 

 

Opsummering

Det bestemte integral giver et tal, som repræsenterer den samlede ændring, akkumulerede mængde eller nettoareal for en funktion mellem to grænser. Det kan findes enten geometrisk som et areal eller algebraisk via stamfunktioner og den fundamentale sætning.