Anvendelser af integralregning

Integraler bruges ikke kun til at beregne arealer, men i mange forskellige sammenhænge hvor man skal opsummere små bidrag til en samlet størrelse. I fysik, økonomi og geometri giver integraler et præcist matematisk værktøj til at måle samlet vækst, energi, masse, afstand eller volumen.

 

 

Areal mellem to kurver

Et af de mest almindelige anvendelser er at finde arealet mellem to funktioner \( \large f(x) \) og \( \large g(x) \). Hvis \( \large f(x) \ge \large g(x) \) i intervallet \([ \large a,\large b ]\), beregnes arealet som forskellen mellem de to:

 

$$ \large A \;=\; \int_a^b \big(f(x) - g(x)\big)\,dx $$

 

 

 

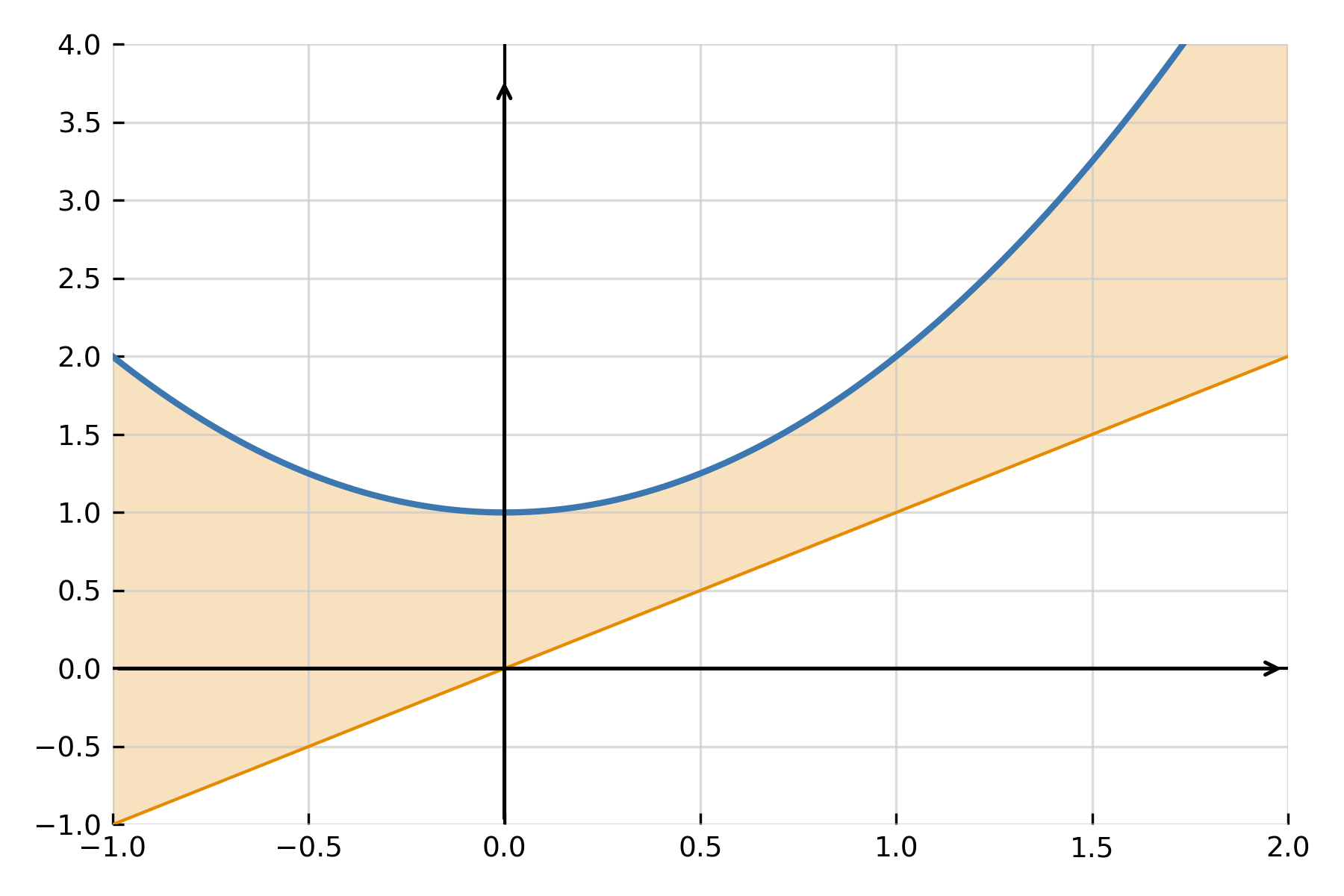
Integralet måler præcis den lodrette afstand mellem kurverne for hvert \( \large x \) og summerer den hen over intervallet. Hvis graferne krydser hinanden, opdeles intervallet i stykker, hvor man tager den positive forskel hver gang.

 

 

Rumfang af omdrejningslegemer

Når en funktion drejes om x-aksen, danner den et tredimensionelt legeme. Rumfanget kan findes ved at summere tværsnitsarealerne (cirkelskiver) langs aksen:

 

$$ \large V \;=\; \pi \int_a^b \big(f(x)\big)^2\,dx $$

 

 

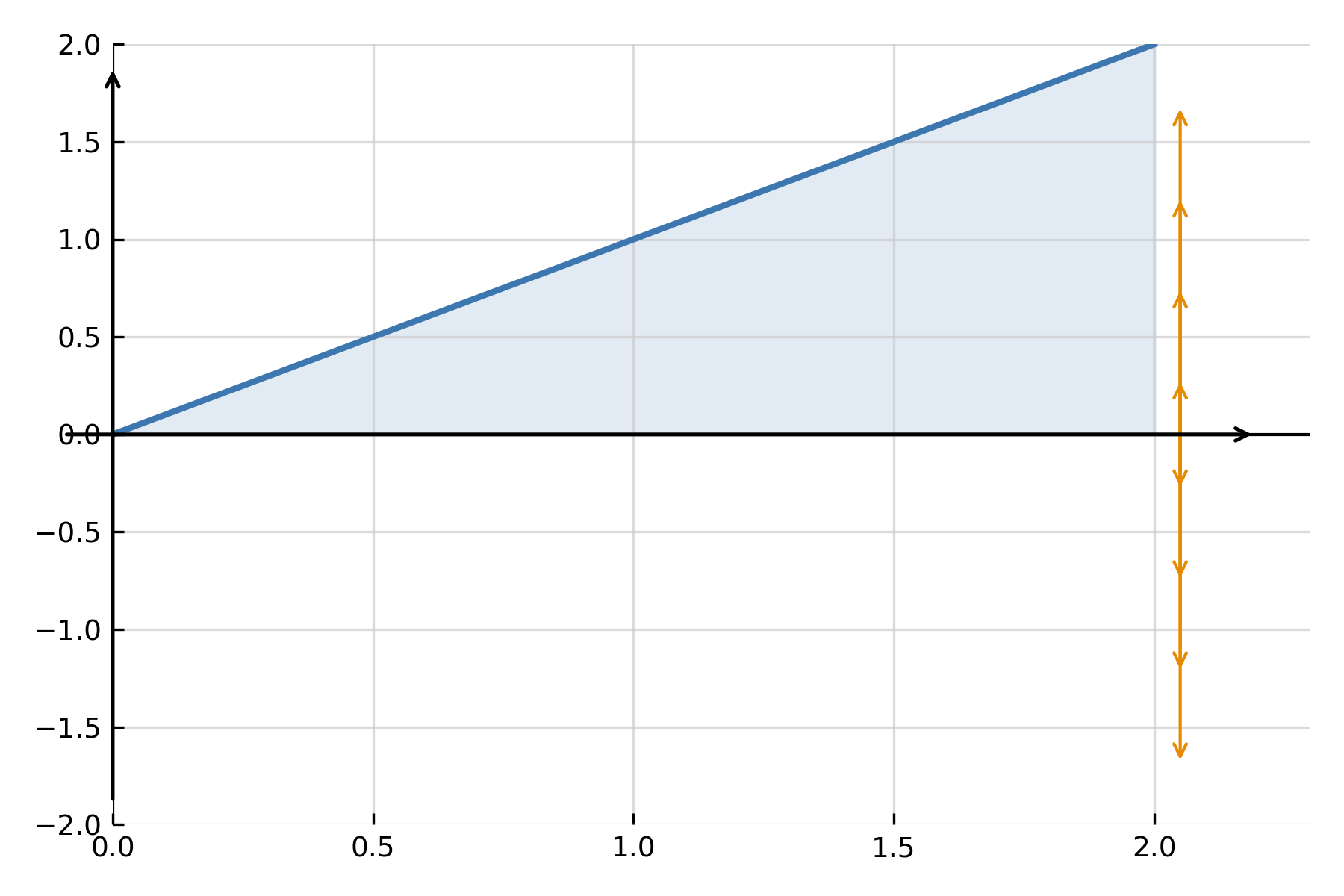
Her er \( \large f(x) \) radius af den roterede funktion ved punktet \( \large x \). Integralet beregner summen af uendeligt mange små cirkelskiver, som tilsammen udgør volumenet.

 

 

Eksempel: Omdrejningslegeme

Find rumfanget af legemet dannet ved at dreje \( \large f(x)=x \) omkring x-aksen fra \( \large x=0 \) til \( \large x=2 \):

 

$$ \large V \;=\; \pi \int_0^2 x^2\,dx \;=\; \pi \Big[\tfrac{1}{3}x^3\Big]_0^2 \;=\; \tfrac{8}{3}\pi $$

 

Det svarer til rumfanget af en kegle med højde 2 og radius 2.

 

 

Arbejde og energi

I fysikken bruges integraler til at beregne arbejde, når en kraft varierer med positionen. Arbejdet \( \large W \) er summen af små kraftbidrag \( \large F(x)\,dx \):

 

$$ \large W \;=\; \int_a^b F(x)\,dx $$

 

Hvis kraften er konstant, reduceres dette til \( \large W = F \cdot s \), men integralen tillader beregning, når kraften ændres langs bevægelsen.

 

 

Bevægelse og tilbagelagt afstand

Når man kender en genstands hastighedsfunktion \( \large v(t) \), giver integralet af \( \large v(t) \) den tilbagelagte strækning:

 

$$ \large s \;=\; \int_{t_1}^{t_2} v(t)\,dt $$

 

Hvis hastigheden kan være negativ (bevægelse tilbage), må man integrere med fortegn. Ønsker man den samlede distance uanset retning, bruges i stedet \( \large \int |v(t)|\,dt \).

 

 

Økonomiske og biologiske anvendelser

Integraler anvendes også til at beregne akkumuleret vækst, forbrug eller indtægt over tid. I økonomi kan \( \large f(x) \) repræsentere en marginal funktion, fx indtægt pr. enhed, og integralet giver den samlede indtjening. I biologi bruges integraler til at måle populationers samlede biomasse, energioptag eller stofmængde.

 

 

Gennemsnitsværdi af en funktion

Gennemsnittet af en funktion på et interval findes ved at tage det samlede areal og dele med intervallets længde:

 

$$ \large f_{\text{avg}} \;=\; \frac{1}{b-a}\int_a^b f(x)\,dx $$

 

Formlen bruges både i statistik, fysik og analyse til at finde middelværdier for kontinuerte funktioner.

 

 

Når et integral ikke kan beregnes analytisk, kan man i stedet bruge numeriske metoder som rektangelmetoden, trapezmetoden eller Simpsons regel til at finde en tilnærmet værdi. Disse metoder beskrives i afsnittet Numeriske metoder.

 

 

Opsummering

Integraler bruges til at beregne arealer, rumfang, energi, arbejde og meget mere. Fælles for alle anvendelser er, at integralet opsummerer små dele til en samlet størrelse. Dermed udgør integralregningen et centralt værktøj til at beskrive og beregne sammenhænge i både natur, teknik og økonomi.