Integralregning

Integralregning handler om at opsummere små bidrag til en samlet størrelse. Hvor differentialregningen måler øjeblikkelige ændringer ($ \large hældninger $), måler integralregningen akkumulerede størrelser som areal, tilbagelagt strækning, samlet vækst eller energi. De to grene hænger tæt sammen: at differentiere og at integrere er omvendte processer.

Hvad er integralregning

Når en størrelse ændrer sig gradvist, kan man forestille sig at dele processen op i mange små bidder og lægge dem sammen. Dette er kernen i integralregning: summen af “små stykker” bliver til en global størrelse. I praksis udtrykkes det gennem integraler.

Geometrisk fortolkning

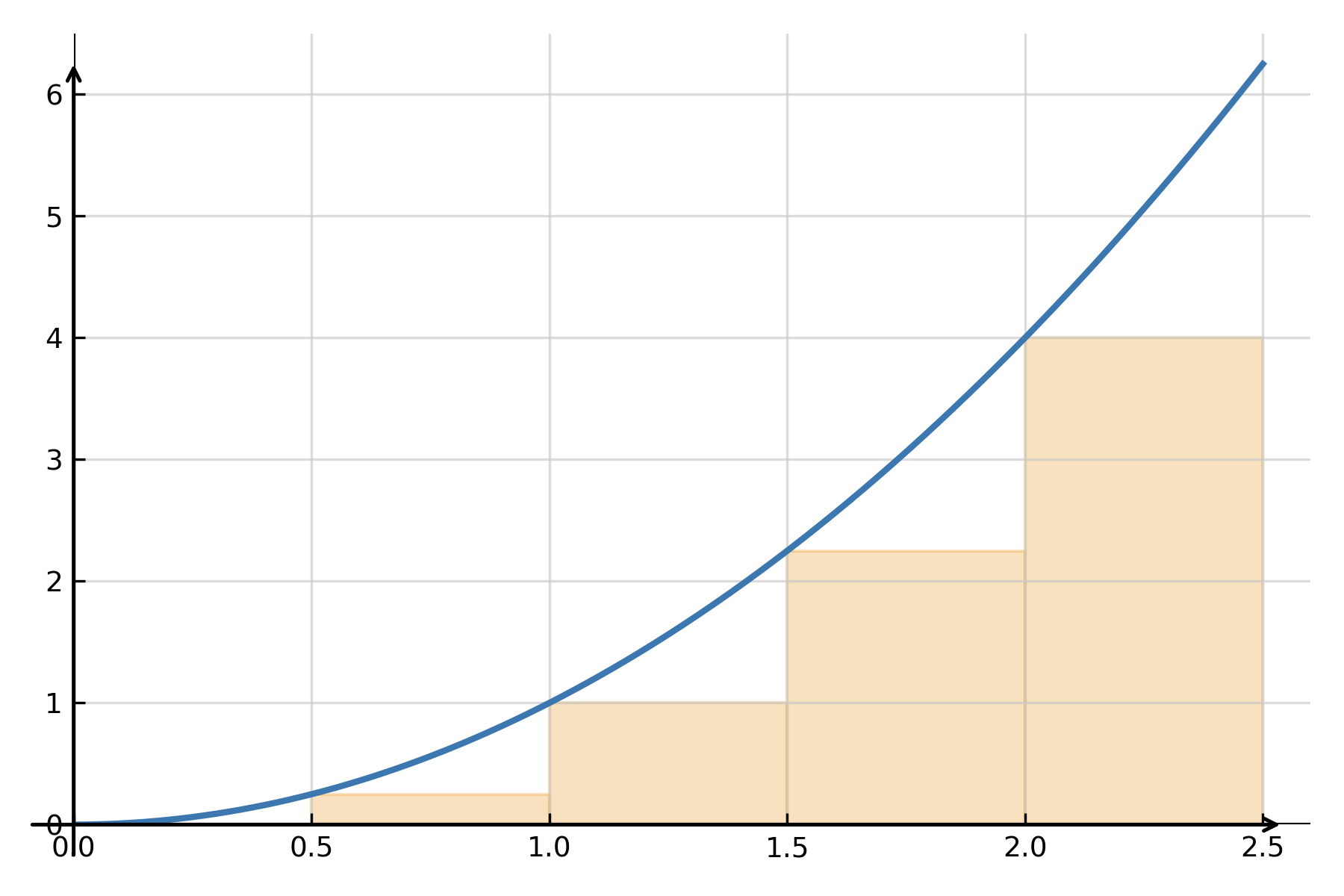
En klassisk fortolkning er arealet under grafen for en ikke-negativ funktion $ \large f(x) $ mellem $ \large x=a $ og $ \large x=b $. Man kan nærme arealet ved at dele intervallet i smalle rektangler, beregne deres arealer og lægge dem sammen. Når bredden går mod nul, nærmer summen sig det præcise areal.

$$ \large \text{Areal} \;=\; \lim_{n \to \infty} \sum_{i=1}^{n} f(x_i)\,\Delta x \;=\; \int_a^b f(x)\,dx $$

Integralet giver altså en præcis måde at måle “akkumuleret størrelse” på, hvad enten det er areal, masse, arbejde eller noget fjerde.

Ubestemt integral (stamfunktion)

Det ubestemte integral repræsenterer “omvendt differentiering”. Hvis $ \large F'(x)=f(x) $, kaldes $ \large F $ en stamfunktion til $ \large f $, og man skriver:

$$ \large \int f(x)\,dx \;=\; F(x) + C $$

Her er $ \large C $ en vilkårlig konstant. Det ubestemte integral beskriver alle funktioner, der har den samme afledte $ \large f $.

Bestemt integral (areal og sum)

Det bestemte integral måler den akkumulerede størrelse mellem to grænser $ \large a $ og $ \large b $. Det defineres som grænsen for Riemann-summerne:

$$ \large \int_a^b f(x)\,dx \;=\; \lim_{n\to\infty}\sum_{i=1}^{n} f(x_i)\,\Delta x $$

Hvis $ \large f \ge 0 $ i intervallet, er dette arealet under grafen. Hvis $ \large f $ skifter fortegn, tælles arealet under x-aksen negativt, hvilket afspejler netto-akkumulationen.

Sammenhængen med differentialregning (Fundamentalsætningen)

Integral- og differentialregning bindes sammen af den fundamentale sætning: Hvis $ \large f $ er kontinuert på $ \large [a,b] $, og $ \large F $ er en stamfunktion til $ \large f $, så gælder:

$$ \large \int_a^b f(x)\,dx \;=\; F(b) - F(a) $$

Det betyder, at et areal (en sum) kan beregnes ved hjælp af en stamfunktion, og at differentiering og integration er omvendte processer.

Eksempler

1. Areal under en simpel funktion

Find $ \large \int_0^2 x\,dx $. En stamfunktion er $ \large F(x)=\tfrac{1}{2}x^2 $, så

$$ \large \int_0^2 x\,dx \;=\; \Big[\tfrac{1}{2}x^2\Big]_0^2 \;=\; \tfrac{1}{2}\cdot 4 - 0 \;=\; 2 $$

2. Akkumuleret afstand fra en hastighedsfunktion

Hvis en bils hastighed er $ \large v(t)=3t $ (m/s), så er den tilbagelagte strækning fra $ \large t=0 $ til $ \large t=4 $:

$$ \large s \;=\; \int_0^4 v(t)\,dt \;=\; \int_0^4 3t\,dt \;=\; \Big[\tfrac{3}{2}t^2\Big]_0^4 \;=\; 24\ \text{m} $$

Her ses, at arealet under hastighedskurven svarer til den samlede tilbagelagte afstand.

Hvorfor to slags integraler

Det ubestemte integral (stamfunktion) er et værktøj til at finde formler og arbejde algebraisk, mens det bestemte integral $ \large måler $ en konkret størrelse på et interval. Den fundamentale sætning lader os oversætte mellem de to perspektiver.

Opsummering

Integralregning handler om at summere små bidrag til en samlet størrelse. Geometrisk tolkes integraler som arealer, fysisk som akkumuleret masse, arbejde eller strækning. Med den fundamentale sætning kan man beregne bestemte integraler via stamfunktioner, og integralregningen fremstår dermed som den naturlige “omvendte” proces til differentialregningen.