Udvidede metoder

Når man først har lært de grundlæggende regneregler, åbner der sig en ny verden af muligheder. Mange funktioner kan ikke skrives direkte som $ \large y = f(x) $, men kan alligevel differentieres ved hjælp af udvidede metoder. De tre vigtigste teknikker er implicit differentiering, parametrisk differentiering og inverse funktioners afledte.

Implicit differentiering

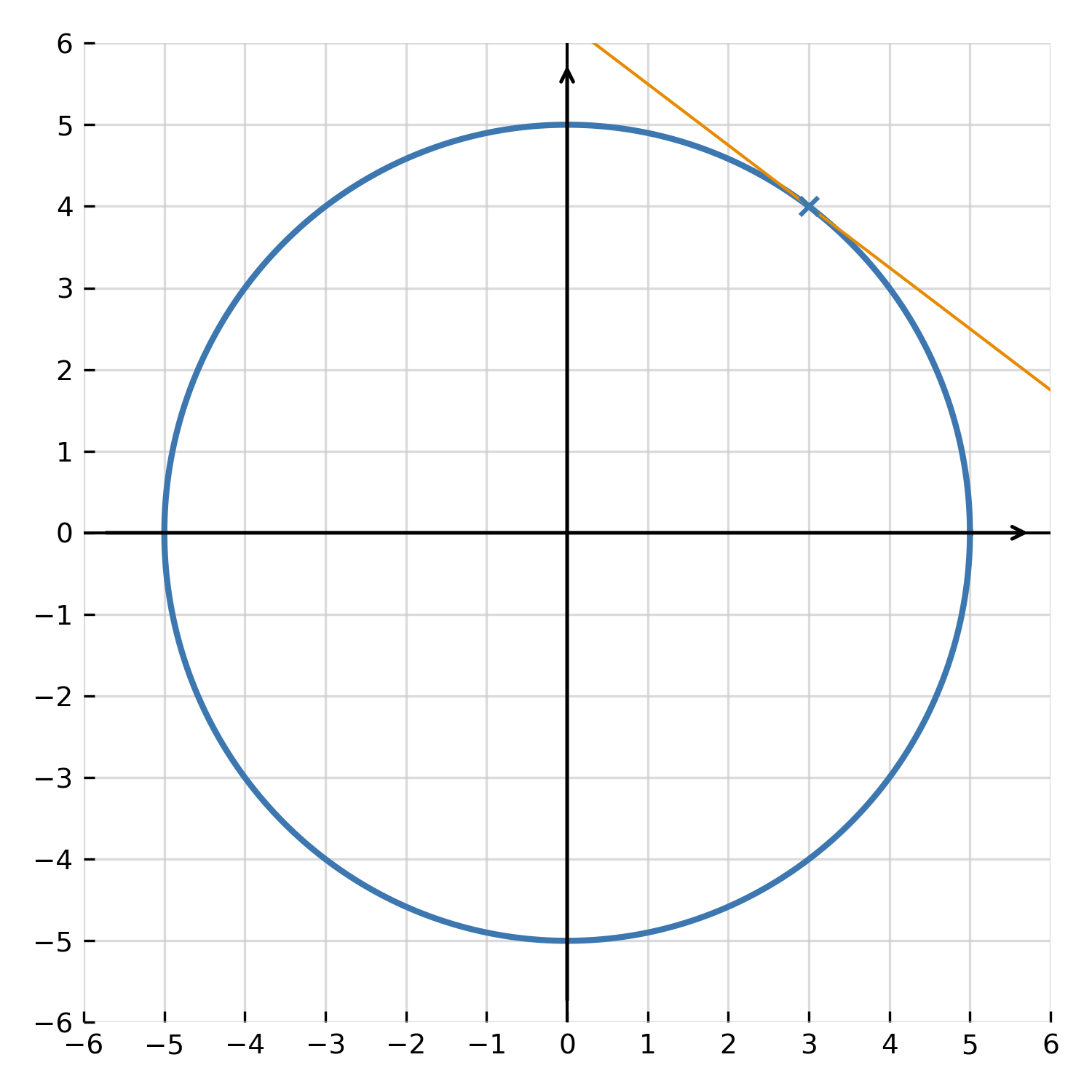
Nogle funktioner er givet ved en ligning, hvor $ \large x $ og $ \large y $ optræder sammen, fx $ \large x^2 + y^2 = 25 $. Man kan ikke isolere $ \large y $ direkte, men man kan finde $ \large \frac{dy}{dx} $ ved at differentiere begge sider med hensyn til $ \large x $ og huske, at $ \large y $ selv afhænger af $ \large x $.

Eksempel:

Differentier $ \large x^2 + y^2 = 25 $ med hensyn til $ \large x $:

$$ \large 2x + 2y \cdot \frac{dy}{dx} = 0 $$

Løs for $ \large \frac{dy}{dx} $:

$$ \large \frac{dy}{dx} = -\frac{x}{y} $$

Dette er hældningen på tangenten til cirklen $ \large x^2 + y^2 = 25 $ i ethvert punkt. Implicit differentiering er særlig nyttig for kurver, der ikke kan beskrives som funktioner i traditionel forstand, fx cirkler, ellipser og hyperbler.

Implicit tangent

Kædereglen i praksis

Kædereglen bruges, når en funktion består af en anden funktion. Den er helt central i alle udvidede metoder. Man kan tænke på den som “én ændring påvirker en anden ændring”.

Eksempel:

Hvis $ \large y = \sin(3x^2) $, så består funktionen af to lag: $ \large \sin(u) $ hvor $ \large u = 3x^2 $. Den afledte findes ved at gange de to ændringsrater:

$$ \large \frac{dy}{dx} = \cos(3x^2) \cdot 6x = 6x \cos(3x^2) $$

Kædereglen kan også bruges flere gange i træk, fx når en funktion er sammensat af tre eller flere lag. Den bliver derfor et uundværligt redskab i alle videregående beregninger.

Parametriske funktioner

Nogle gange er både $ \large x $ og $ \large y $ givet som funktioner af en tredje variabel, ofte kaldet $ \large t $ (parameteren). Det ses fx i bevægelseslære, hvor en partikel bevæger sig i rummet, og man kender dens position som funktion af tiden.

Hvis $ \large x = x(t) $ og $ \large y = y(t) $, kan man finde den afledte $ \large \frac{dy}{dx} $ ved at kombinere de to afledte i forhold til $ \large t $:

$$ \large \frac{dy}{dx} = \frac{\frac{dy}{dt}}{\frac{dx}{dt}} $$

Eksempel:

Hvis $ \large x = t^2 $ og $ \large y = 3t + 1 $, så gælder

$$ \large \frac{dx}{dt} = 2t \qquad \text{og} \qquad \frac{dy}{dt} = 3 $$

Dermed fås

$$ \large \frac{dy}{dx} = \frac{3}{2t} $$

Dette udtryk viser hældningen på kurven i det punkt, som svarer til parameteren $ \large t $.

Inverse funktioner

Hvis en funktion har en invers, kan man også finde den afledte af den inverse uden først at bestemme den eksplicit. Lad $ \large y = f(x) $ være en differentierbar funktion med en invers $ \large x = f^{-1}(y) $. Så gælder sammenhængen:

$$ \large \frac{dy}{dx} = f'(x) \quad \Rightarrow \quad \frac{dx}{dy} = \frac{1}{f'(x)} $$

Med andre ord: den afledte af den inverse funktion er den reciprokke værdi af den oprindelige funktions afledte.

Eksempel:

Hvis $ \large f(x) = e^x $, så er $ \large f^{-1}(x) = \ln(x) $. Da $ \large f'(x) = e^x $, følger:

$$ \large (\ln x)' = \frac{1}{e^x} = \frac{1}{x} $$

Dette stemmer overens med den kendte afledte af logaritmen og viser princippet i praksis.

Kombinerede metoder

Ofte møder man funktioner, hvor flere af disse teknikker skal bruges sammen — fx en implicit ligning, hvor en parameter indgår, eller en sammensat funktion, der skal inverteres. Den erfarne regner lærer at kombinere reglerne naturligt:

$$ \large \frac{dy}{dx} = \frac{dy}{dt} \cdot \frac{dt}{dx} $$

Dette er i virkeligheden bare en udvidet udgave af kædereglen, hvor man kan skifte mellem variable efter behov.

Opsummering

De udvidede metoder gør det muligt at differentiere funktioner, som ikke kan skrives på simpel form. Implicit differentiering bruges til relationer mellem $ \large x $ og $ \large y $, parametrisk differentiering anvendes, når begge afhænger af en parameter, og reglen for inverse funktioner gør det muligt at finde afledte af logaritmer og inverse trigonometriske funktioner. Disse værktøjer udvider differentialregningens rækkevidde og danner grundlag for mere avancerede emner i analysen.