Den afledte funktion
Den afledte funktion fortæller, hvor hurtigt en anden funktion ændrer sig. Hvis \( \large f(x) \) beskriver en størrelse, angiver den afledte \( \large f'(x) \), hvor meget denne størrelse ændres, når \( \large x \) ændres en lille smule. På den måde bliver differentialregning et præcist værktøj til at måle forandringer.
Fra sekant til tangent
For at forstå, hvad det betyder at “differentere”, begynder man med hældningen af en sekant. En sekant er den rette linje, som forbinder to punkter på grafen for \( \large f(x) \). Hældningen af sekanten fortæller, hvor meget funktionen i gennemsnit stiger eller falder mellem de to punkter.
$$ \large a_{\text{sekant}} = \frac{f(x+h) - f(x)}{h} $$
Hvis man vælger punkterne tættere og tættere på hinanden, så \( \large h \) bliver meget lille, nærmer sekanten sig en linje, der kun rører grafen i ét punkt — tangentlinjen. Hældningen på denne tangent kaldes den øjeblikkelige ændringsrate. Det er netop den værdi, som den afledte funktion giver os.
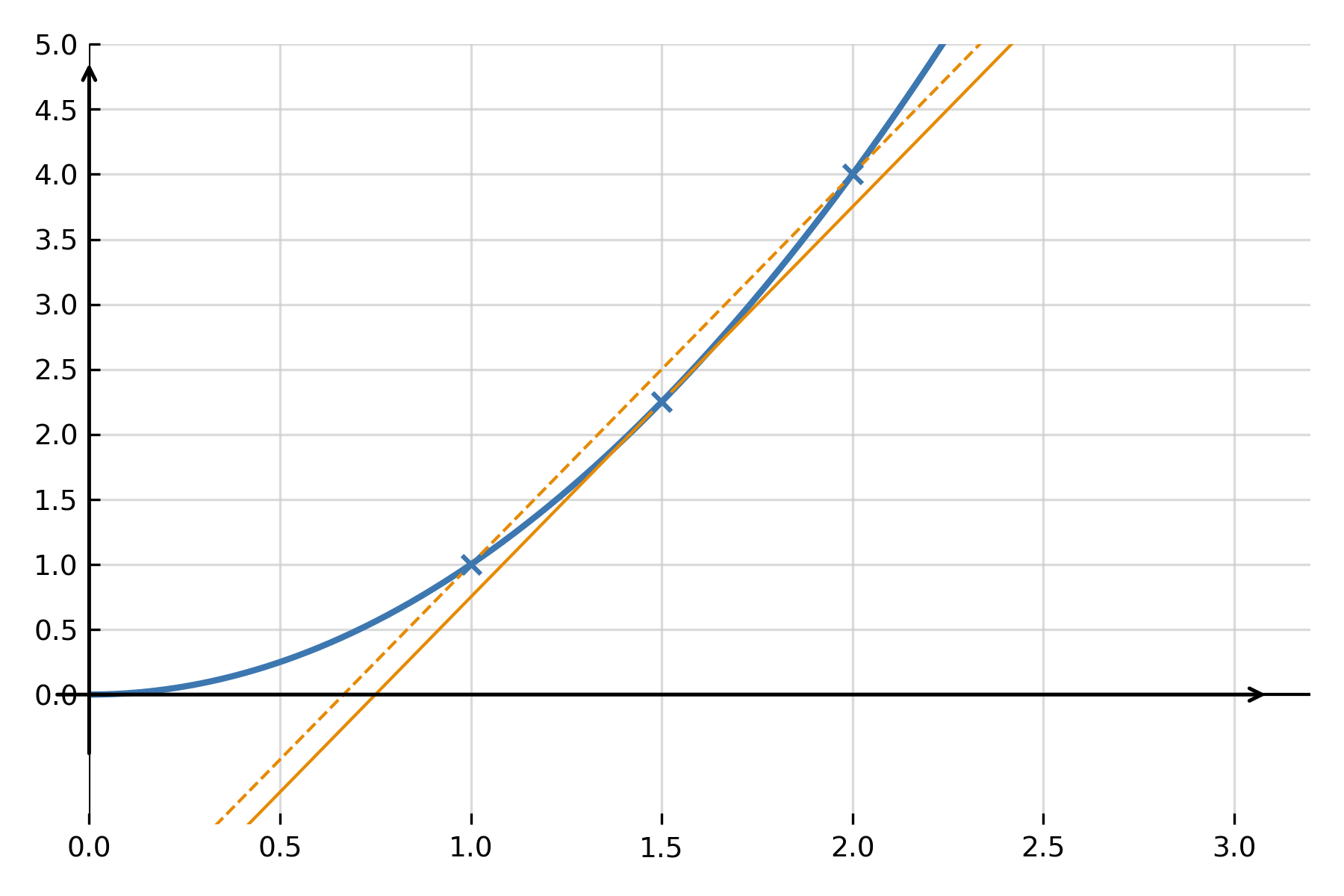
Definition via grænseværdi
Den præcise definition af den afledte funktion er:
$$ \large f'(x) = \lim_{h \to 0} \frac{f(x+h) - f(x)}{h} $$
Her måler brøken, hvor meget \( \large f(x) \) ændrer sig, når \( \large x \) ændres med et lille tal \( \large h \). Når \( \large h \) går mod nul, får man ændringen i præcis det punkt — tangentens hældning. Grænseværdien findes kun, hvis funktionen er glat nok i punktet, dvs. at der ikke er spring, spidser eller knæk.
Notation og læsning
Der findes flere måder at skrive den afledte på:
$$ \large f'(x) \quad \text{eller} \quad \frac{dy}{dx} \quad \text{eller} \quad Df(x) $$
Alle tre betyder det samme: hvor meget \( \large y \) ændres, når \( \large x \) ændres. I fysikken læser man fx \( \large \frac{dy}{dt} \) som “ændringen i afstand over ændringen i tid”, altså hastighed.
Grafisk forståelse
Den afledte funktion giver en ny funktion, som i hvert punkt fortæller hældningen på grafen for \( \large f(x) \). Hvor grafen stiger, er den afledte positiv; hvor den falder, er den afledte negativ; og hvor grafen har en vandret tangent, er den afledte nul.
Et punkt hvor \( \large f'(x) = 0 \) kaldes et stationært punkt. Sådanne punkter spiller en vigtig rolle senere, når man skal finde maksimum og minimum for funktioner.
Fysisk fortolkning
I mange sammenhænge repræsenterer den afledte en fysisk størrelse. Hvis \( \large f(x) \) beskriver en position som funktion af tiden, så er \( \large f'(x) \) hastigheden — hvor hurtigt man bevæger sig. Hvis man differentierer én gang til, får man accelerationen, \( \large f''(x) \), som viser, hvor hurtigt hastigheden selv ændrer sig.
Eksempler
1. Eksempel – kvadratfunktion
For \( \large f(x) = x^2 \) kan man beregne den afledte direkte ud fra definitionen:
$$ \large f'(x) = \lim_{h \to 0} \frac{(x+h)^2 - x^2}{h} = \lim_{h \to 0} \frac{2xh + h^2}{h} = 2x $$
Den afledte funktion er \( \large f'(x) = 2x \). Hældningen afhænger altså af, hvor man befinder sig på grafen. I punktet \( \large x = 3 \) er hældningen \( \large f'(3) = 6 \).
2. Eksempel – lineær funktion
For \( \large f(x) = 5x + 2 \) er grafen allerede en ret linje. Dens hældning er konstant, og den afledte bliver derfor:
$$ \large f'(x) = 5 $$
Her ændrer funktionen sig altid med 5 enheder opad, når \( \large x \) øges med 1. Det viser, at differentialregning generaliserer den velkendte hældningsidé fra ret linjer til alle glatte funktioner.
3. Eksempel – fysisk tolkning
Hvis \( \large s(t) = t^2 \) beskriver en bils tilbagelagte afstand i meter som funktion af tiden \( \large t \) i sekunder, så er hastigheden \( \large v(t) = s'(t) = 2t \). Efter 4 sekunder kører bilen altså med \( \large v(4) = 8 \) m/s. Den afledte giver her et direkte mål for bevægelsens hastighed.
Mini-regneregler
Når man skal finde afledte af almindelige funktioner, gælder nogle enkle regler:
$$ \large (k)' = 0 \qquad (x^n)' = n \cdot x^{n-1} \qquad (k \cdot f(x))' = k \cdot f'(x) $$
Disse danner grundlaget for de generelle regneregler, som behandles i næste afsnit. Med dem kan man differentiere selv meget sammensatte funktioner uden at gå tilbage til grænseværdidefinitionen.
Opsummering
Den afledte funktion udtrykker, hvor hurtigt en funktion ændrer sig i hvert punkt. Den kan forstås som hældningen på tangentlinjen, som et mål for ændringshastighed eller som et matematisk redskab til at beskrive bevægelse og vækst. Den spiller en central rolle i næsten alle områder af matematik, fysik og økonomi.