Linearisering og approksimation

Differentialregning gør det muligt at forstå og tilnærme funktioner lokalt. Når en funktion er glat og differentierbar, kan man i et lille område omkring et punkt erstatte den med en ret linje – nemlig tangentlinjen. Denne metode kaldes linearisering og bruges til at finde hurtige tilnærmelser, når præcise beregninger er besværlige eller unødvendige.

Idéen bag linearisering

I nærheden af et punkt $ \large x_0 $ opfører en differentiabel funktion $ \large f(x) $ sig næsten som sin tangent. Hvis man kender funktionen og dens afledte i det punkt, kan man derfor beskrive hele dens lokale forløb ved en lineær funktion, som er nem at regne med.

Den lineære approksimation (tangentligningen) har formen:

$$ \large f(x) \approx f(x_0) + f'(x_0) \cdot (x - x_0) $$

Dette udtryk siger, at funktionsværdien i et punkt tæt på $ \large x_0 $ kan tilnærmes ved værdien i $ \large x_0 $ plus ændringen givet af hældningen $ \large f'(x_0) $. Jo tættere $ \large x $ ligger på $ \large x_0 $, desto bedre virker tilnærmelsen.

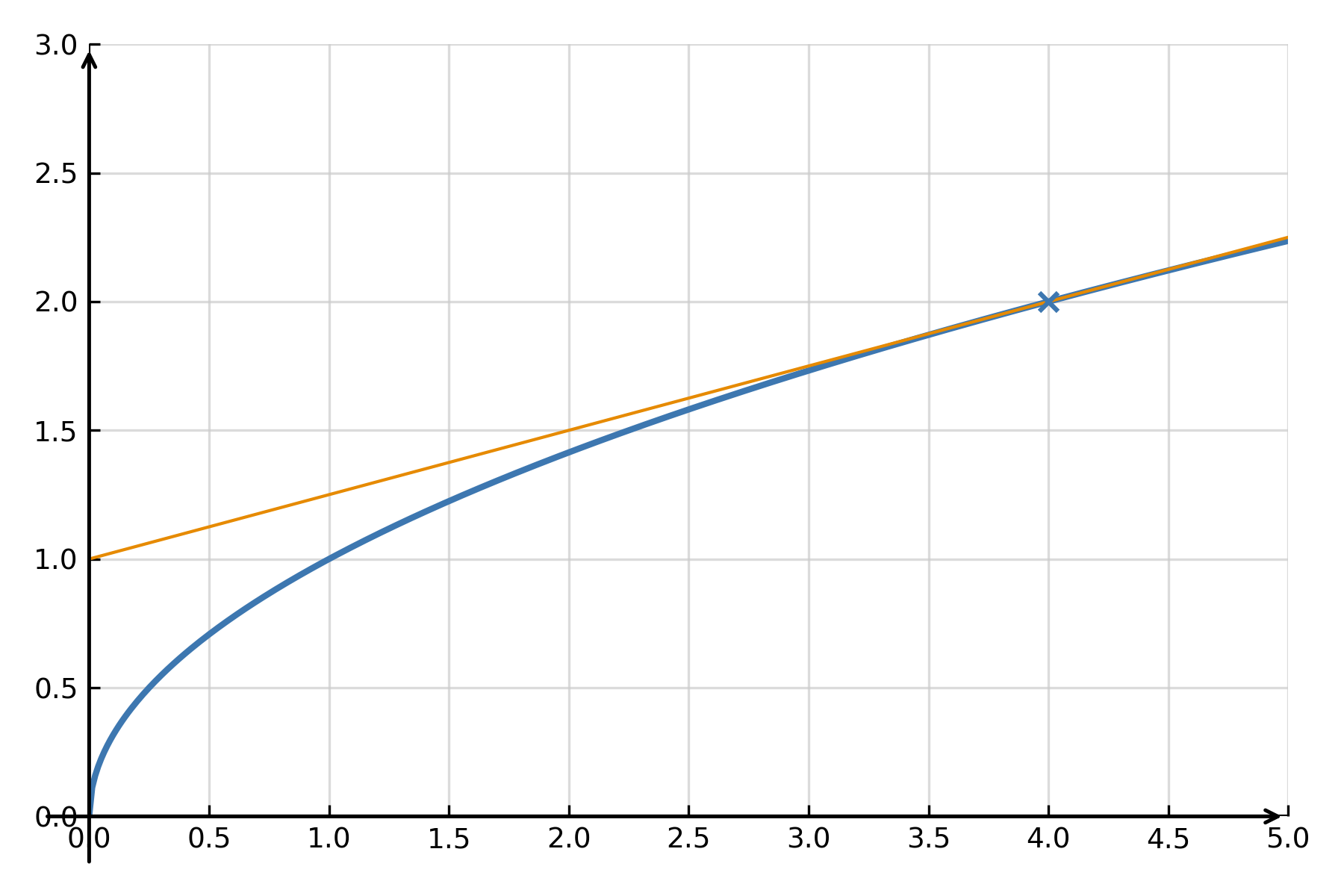
Linearisering tangent

Grafisk forståelse

Tangentlinjen “rører” grafen for $ \large f(x) $ i ét punkt og følger dens retning dér. For små ændringer i $ \large x $ ligger funktionen og tangenten næsten oven på hinanden. Linearisering betyder derfor, at man erstatter en krum kurve med dens lokale rette linje. Det gør beregninger meget enklere uden at miste nøjagtigheden i det område.

Eksempel 1: Linearisering af en kvadratfunktion

Find den lineære approksimation til $ \large f(x) = x^2 $ omkring punktet $ \large x_0 = 2 $.

Man har $ \large f(2) = 4 $ og $ \large f'(x) = 2x $, så $ \large f'(2) = 4 $. Dermed:

$$ \large f(x) \approx 4 + 4(x - 2) = 4x - 4 $$

Når $ \large x $ ligger tæt på 2, kan man altså bruge $ \large 4x - 4 $ som en god tilnærmelse til $ \large x^2 $. For eksempel giver $ \large f(2.1) \approx 4.4 $, mens det sande resultat er $ \large 2.1^2 = 4.41 $.

Eksempel 2: Approksimation af en rod

Man kan bruge linearisering til at beregne kvadratrodstilnærmelser uden lommeregner. For eksempel kan $ \large \sqrt{4.1} $ findes ved at linearisere funktionen $ \large f(x) = \sqrt{x} $ omkring $ \large x_0 = 4 $.

Her gælder $ \large f(4) = 2 $ og $ \large f'(x) = \frac{1}{2\sqrt{x}} $, så $ \large f'(4) = \frac{1}{4} $.

$$ \large f(x) \approx 2 + \frac{1}{4}(x - 4) $$

For $ \large x = 4.1 $: $ \large f(4.1) \approx 2 + \frac{1}{4} \cdot 0.1 = 2.025 $, mens den præcise værdi er $ \large 2.0248 $. Tangenttilnærmelsen giver altså et resultat med næsten ingen fejl.

Fejl og nøjagtighed

Jo tættere $ \large x $ er på $ \large x_0 $, desto bedre virker tilnærmelsen. Hvis man bevæger sig længere væk, begynder tangentlinjen at afvige fra den oprindelige kurve, fordi højere ordens ændringer (krumningen) får betydning. Dette kan korrigeres ved at inddrage flere led i en Taylor-udvikling.

I første orden svarer linearisering til den første del af Taylor-rækken:

$$ \large f(x) = f(x_0) + f'(x_0)(x - x_0) + \frac{f''(x_0)}{2!}(x - x_0)^2 + \dots $$

Når man kun tager det første led efter $ \large f(x_0) $, får man netop tangenttilnærmelsen. Derfor kaldes metoden også første ordens Taylor-approksimation.

Eksempel 3: Fysisk fortolkning

I fysik bruges linearisering til at beskrive bevægelser eller processer i små tidsintervaller. Hvis $ \large s(t) $ beskriver en position, så kan den lineære tilnærmelse

$$ \large s(t) \approx s(t_0) + v(t_0) \cdot (t - t_0) $$

tolkes som: “den nye position er den gamle plus hastighed gange tid”. Her spiller hastigheden $ \large v(t_0) = s'(t_0) $ præcist samme rolle som tangentens hældning i matematikken.

Opsummering

Linearisering gør det muligt at erstatte en funktion med en simpel lineær model omkring et givet punkt. Tangentlinjen fungerer som en lokal tilnærmelse, der er hurtig at regne med og ofte tilstrækkelig præcis. Metoden danner grundlaget for mange numeriske procedurer og for Taylor-udviklingen, som udvider idéen til mere nøjagtige approksimationer.